某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y＝－2x＋100．（利润＝售价－制造成本）
(1)写出每月的利润Ｗ（万元）与销售单价x（元）之间的函数关系式；
(2)当销售单价为多少元时，厂商每月获得的利润为440万元？
(3)根据相关部门规定，这种电子产品的销售单价不能高于40元，如果厂商每月的制造成本不超过540万元，那么当销售单价为多少元时，厂商每月获得的利润最大？最大利润为多少万元？
科目：初中数学 来源： 题型：
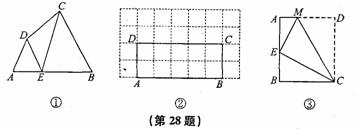
如图①，在四边形ABCD的边AB上任取一点E（点E不与点A、点B重合），分别连接ED、EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把点E叫做四边形ABCD的边AB上的相似点；如果这三个三角形都相似，我们就把点E叫做四边形ABCD的边AB上的强相似点，解决问题：
(1)如图①，∠A＝∠B＝∠DEC＝55°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由；
(2)如图②，在矩形ABCD中，AB＝5，BC＝2，且A、B、C、D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图②中画出矩形ABCD的边AB上的一个强相似点E；
拓展探究：
(3)如图③，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处．若点E恰好是四边形ABCM的边AB上的一个强相似点，试探究AB和BC的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
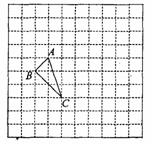
如图，正方形网格中每个小正方形边长都是1，每个小格的顶点叫格点，以格点为顶点的三角形叫做格点三角形．
(1)求格点三角形ABC的面积；
(2)在网格图中画出△ABC先向右平移4个单位，再向上平移
3个单位后的△A1B1C1；
(3)画出格点三角形ABC绕点C逆时针旋转90°后的△A2B2C2
．
查看答案和解析>>
科目：初中数学 来源： 题型：
下列说法正确的是 ( )
A．某种彩票的中奖机会是1%，则买100张这种彩票一定会中奖
B．为了解全国中学生的睡眠情况，应该采用普查的方式
C．－组数据3，5，4，5，5，6，10的众数和中位数都是5
D．若甲组数据的方差s
＝0.05，乙组数据的方差s
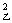＝0.1，则乙组数据比甲组数据稳定
查看答案和解析>>
科目：初中数学 来源： 题型：
2014年3月14日，“玉兔号”月球车成功在距地球约384 400公里远的月球上自主唤醒，将384 400精确到万位用科学记数法表示为_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
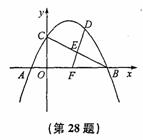
如图，二次函数y＝ax2＋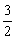
x＋c（a≠0）的图像与x轴交于A、B两点，与y轴交于点C，已知点A（－1，0），点C(0，2)．
(1)求抛物线的函数解析式，并求出该抛物线的顶点坐标；
(2)若点D是抛物线在第一象限的部分上的一动点，
①当四边形OCDB的面积最大时，求点D的坐标；
②若E为BC的中点，DE的延长线交线段AB于点F，当△BEF为钝角三角形时，请直接写出点D的纵坐标y的范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中自变量x的取值范围是 ．