
如图1是一张折叠椅子,图2是其侧面示意图,已知椅子折叠时长1.2米,椅子展开后最大张角∠CBD=37°,且BD=BC,AB:BG:GC=1:2:3,座面EF与地面平行,当展开角最大时,请解答下列问题:
(1)求∠CGF的度数;
(2)求座面EF与地面之间的距离。(可用计算器计算,结果保留两个有效数字,参考数据:sin71.5°≈0.948,cos71.5°≈0.317,tan71.5°≈2.989

(1)∠CGF=71.5°(2)0.57m
【解析】
试题分析:此题考查了等腰三角形的性质、三角形内角和定理、平行线的性质和三角函数的基本概念,主关键把实际问题转化为数学问题加以计算.(1)根据等腰三角形的性质和三角形内角和定理可得∠BCD的度数,再根据平行线的性质可得∠CGF的度数;(2)根据比的意义可得GC=1.2×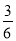 =0.6m,过点G作GK⊥DC于点K,在Rt△KCG中,根据三角函数可得座面EF与地面之间的距离.
=0.6m,过点G作GK⊥DC于点K,在Rt△KCG中,根据三角函数可得座面EF与地面之间的距离.
试题解析:(1)∵BD=BC,∠CBD=37°,∴∠BDC=∠BCD=(180°-37°)÷2=71.5°
∵EF∥DC ∴∠CGF=∠BCD=71.5°
(2)
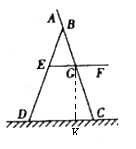
过点G作GK⊥DC于点K. ∵BD=BC,AB:BG:GC=1:2:3 ∴GC=1.2×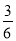 =0.6m
=0.6m
在Rt△KCG中, sin71.5°=GK/CF=GK/0.6=0.948 GK=0.57m.
答:座面EF与地面之间的距离约是0.57m.
考点:解直角三角形的应用.


科目:初中数学 来源:2015届北京市大兴区八年级下学期期末考试数学试卷(解析版) 题型:填空题
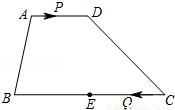
如图,在梯形ABCD中,AD∥BC,AD=4,BC=12,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间为 2或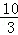 秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源:2015届云南省八年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,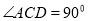 ,
,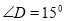 ,B点在AD的垂直平分线上,若AC=4,则BD等于( )
,B点在AD的垂直平分线上,若AC=4,则BD等于( )
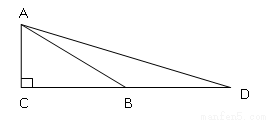
A、10 B、8 C、6 D、4
查看答案和解析>>
科目:初中数学 来源:2015届云南省八年级上学期期末考试数学试卷(解析版) 题型:选择题
下列长度的三条线段,能组成等腰三角形的是( )
A、1,1,2 B、2,2,5 C、3,3,5 D、3,4,5
查看答案和解析>>
科目:初中数学 来源:2014年江西省吉安市吉州区九年级下学期第一次中考模拟数学试卷(解析版) 题型:填空题
“Welcome to Senior High School.”(高中欢迎你),在这段句子的所有英文字母中,字母o出现的频率是___________。
查看答案和解析>>
科目:初中数学 来源:2014年北京市西城区中考二模数学试卷(解析版) 题型:解答题
列方程或方程组解应用题:
一列“和谐号”动车组,有一等车厢和二等车厢共6节,一共设有座位496个.其中每节一等车厢设有座位64个,每节二等车厢设有座位92个.问该列车一等车厢和二等车厢各有多少节?
查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考二模数学试卷(解析版) 题型:解答题
如果一条抛物线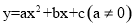 与
与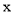 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是 三角形;
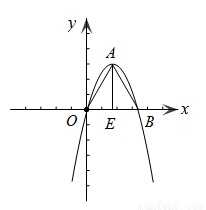
(2)如图,△OAB是抛物线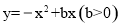 的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
(3)在(2)的条件下,若以点E为圆心,r为半径的圆与线段AD只有一个公共点,求出r的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com