
如果一条抛物线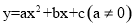 与
与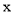 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是 三角形;
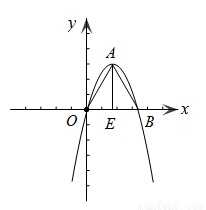
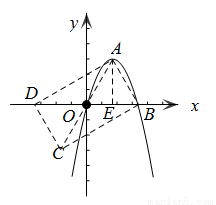
(2)如图,△OAB是抛物线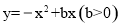 的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
(3)在(2)的条件下,若以点E为圆心,r为半径的圆与线段AD只有一个公共点,求出r的取值范围.
(1)等腰;(2)存在,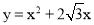 ;(3)
;(3)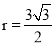 或
或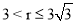 .
.
【解析】
试题分析:(1)根据抛物线的轴对称性和等腰三角形的判定可得结论.
(2)根据“抛物线三角形”求出A,B的坐标,求出A,B关于原点O为对称的点C,D的坐标,根据待定系数法求出过O、C、D三点的抛物线的表达式.
(3)点E为圆心,r为半径的圆与线段AD只有一个公共点,则⊙E与AD相切或⊙E的半径在AE和AD之间.
(1)等腰 .
(2)存在.
如图,作△OCD与△OAB关于原点O中心对称,则四边形ABCD为平行四边形.
当OA=OB时,平行四边形ABCD为矩形 .
又∵AO=AB,∴△OAB为等边三角形.
作AE⊥OB,垂足为E.
∴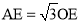 .∴
.∴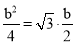 (b﹥0).∴
(b﹥0).∴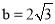 .
.
∴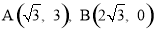 .
.
∴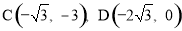 .
.
设过点O,C,D三点的抛物线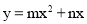 ,则
,则
 ,解之,得
,解之,得 .
.
∴所求抛物线的表达式为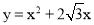 .
.
(3)①⊙E与AD相切时, 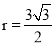 .
.
②⊙E过点D时,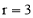 .
.
③⊙E过点A时,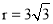 .
.
综上所述,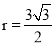 或
或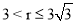 .
.
考点:1.新定义;2.二次函数的性质;3.等腰三角形的判定;4.关于坐标原点对称的性质;5.待定系数法的应用;6.曲线上点的坐标与方程的关系;7.直线与圆的位置关系;8.分类思想的应用.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源:2014年江西省吉安市吉州区九年级下学期第一次中考模拟数学试卷(解析版) 题型:解答题
如图1是一张折叠椅子,图2是其侧面示意图,已知椅子折叠时长1.2米,椅子展开后最大张角∠CBD=37°,且BD=BC,AB:BG:GC=1:2:3,座面EF与地面平行,当展开角最大时,请解答下列问题:
(1)求∠CGF的度数;
(2)求座面EF与地面之间的距离。(可用计算器计算,结果保留两个有效数字,参考数据:sin71.5°≈0.948,cos71.5°≈0.317,tan71.5°≈2.989

查看答案和解析>>
科目:初中数学 来源:2014年北京市西城区中考二模数学试卷(解析版) 题型:选择题
在一个不透明的口袋中装有5张完全相同的卡片,卡片上面分别写有数字-2,-1,0, 1,3,从中随机抽出一张卡片,卡片上面的数字是负数的概率为( )
A.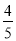 B.
B.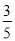 C.
C. D.
D.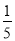
查看答案和解析>>
科目:初中数学 来源:2014年北京市海淀区中考二模数学试卷(解析版) 题型:填空题
平面直角坐标系中有一点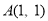 ,对点
,对点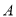 进行如下操作:
进行如下操作:
第一步,作点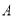 关于
关于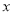 轴的对称点
轴的对称点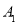 , 延长线段
, 延长线段 到点
到点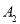 ,使得
,使得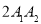 =
= ;
;
第二步,作点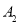 关于
关于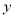 轴的对称点
轴的对称点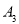 , 延长线段
, 延长线段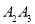 到点
到点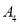 ,使得
,使得 ;
;
第三步,作点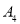 关于
关于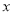 轴的对称点
轴的对称点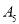 , 延长线段
, 延长线段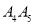 到点
到点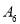 ,使得
,使得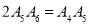 ;
;
·······
则点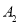 的坐标为________,点
的坐标为________,点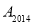 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源:2014年北京市海淀区中考二模数学试卷(解析版) 题型:选择题
掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷一次骰子,在骰子向上的一面上出现点数大于4的概率为( )
A. B.
B. C.
C.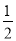 D.
D.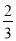
查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考二模数学试卷(解析版) 题型:解答题
房山某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“最喜欢哪种学习方式” 随机调查了他们周围的一些同学,根据收集到的数据绘制了以下的两个统计图.请根据下面两个不完整的统计图回答以下问题:
(1)这次抽样调查中,共调查了 名学生;
(2)补全两幅统计图;
(3)根据抽样调查的结果,估算该校1000名学生中大约有多少人选择“小组合作学习”?

查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:解答题
如图, AE是⊙O直径,D是⊙O上一点,连结AD并延长使AD=DC,连结CE交⊙O于点B,连结AB.过点E的直线与AC的延长线交于点F,且∠F=∠CED.
(1)求证:EF是⊙O切线;
(2)若CD=CF=2,求BE的长.

查看答案和解析>>
科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:选择题
如图,铁路道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高(杆的宽度忽略不计)( )

A.4m B.6m C.8m D.12m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com