
如图, AE是⊙O直径,D是⊙O上一点,连结AD并延长使AD=DC,连结CE交⊙O于点B,连结AB.过点E的直线与AC的延长线交于点F,且∠F=∠CED.
(1)求证:EF是⊙O切线;
(2)若CD=CF=2,求BE的长.

(1)证明见解析;(2)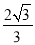 .
.
【解析】
试题分析:(1)根据圆周角定理由AE是⊙O直径得到∠ADE=90°,而AD=DC,根据等腰三角形的判定方法得到EA=EC,则∠AED=∠CED,由于∠F=∠CED,所以∠AED=∠F,易得∠F+∠EAD=90°,即∠AEF=90°,然后根据切线的判定定理即可得到EF是⊙O切线;
(2)根据相似三角形的判定方法得到△ADE∽△AEF,利用相似比可计算出AE=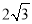 ,则CE=AE=
,则CE=AE=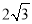 ,在Rt△ADE中,利用勾股定理计算出DE=
,在Rt△ADE中,利用勾股定理计算出DE=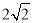 ,再由AE是⊙O直径得到∠ABE=90°,则根据面积法得到
,再由AE是⊙O直径得到∠ABE=90°,则根据面积法得到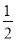 CE•AB=
CE•AB=
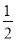 DE•AC,则可计算出AB=
DE•AC,则可计算出AB=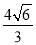 ,,然后在Rt△ABE中,根据勾股定理计算BE.
,,然后在Rt△ABE中,根据勾股定理计算BE.
试题解析:(1)证明:∵AE是⊙O直径,∴∠ADE=90°.∴ED⊥AC.
∵AD=DC,∴EA=EC.∴∠AED=∠CED,
∵∠F=∠CED,∴∠AED=∠F.
而∠AED+∠EAD=90°,∴∠F+∠EAD=90°.∴∠AEF=90°.∴AE⊥EF.
∴EF是⊙O切线.
(2)∵CD=CF=2,∴AD=CD=CF=2.
∵∠ADE=∠AEF,∠DAE=∠EAF,∴△ADE∽△AEF.
∴AE:AF=AD:AE,即AE:6=2:AE.∴AE=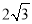 .∴CE=AE=
.∴CE=AE=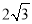 .
.
在Rt△ADE中, .
.
∵AE是⊙O直径,∴∠ABE=90°.
∴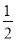 CE•AB=
CE•AB=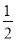 DE•AC,∴AB=
DE•AC,∴AB=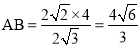 .
.
在Rt△ABE中,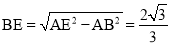 .
.
考点:1.切线的判定和性质;2.相似三角形的判定和性质;3.圆周角定理;4勾股定理;5.等腰三角形的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014年北京市西城区中考二模数学试卷(解析版) 题型:解答题
列方程或方程组解应用题:
一列“和谐号”动车组,有一等车厢和二等车厢共6节,一共设有座位496个.其中每节一等车厢设有座位64个,每节二等车厢设有座位92个.问该列车一等车厢和二等车厢各有多少节?
查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考二模数学试卷(解析版) 题型:解答题
如果一条抛物线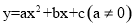 与
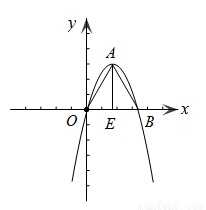
与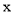 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是 三角形;
(2)如图,△OAB是抛物线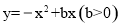 的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
(3)在(2)的条件下,若以点E为圆心,r为半径的圆与线段AD只有一个公共点,求出r的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考二模数学试卷(解析版) 题型:选择题
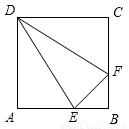
如图,正方形ABCD的边长为4,点E,F分别为边AB,BC上的动点,且DE=DF.若△DEF的面积为y,BF的长为x,则表示y与x的函数关系的图象大致是( )
A.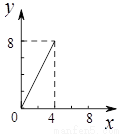 B.
B.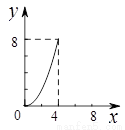 C.
C.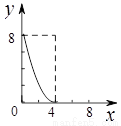 D.
D.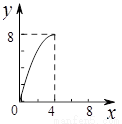
查看答案和解析>>
科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:解答题
列方程或方程组解应用题
某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.求原计划每天生产多少台机器.
查看答案和解析>>
科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:选择题
西部大开发战略是党中央面向21世纪的重大决策,我国西部地区面积为6 400 000平方千米,将6 400 000用科学记数法表示应为( )
A. B.
B. C.
C.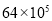 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com