
【题目】如图,在ABCD中,对角线AC,BD相交于O,E,F是对角线上的两点,给出下列四个条件:①OE=OF;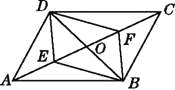
②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.0个
B.1个
C.2个
D.3个
【答案】B
【解析】解:①∵ABCD,∴OB=OD
∵OE=OF
∴四边形DEBF是平行四边形,因此①不符合题意;
②DE=BF不能判断四边形DEBF是平行四边形,因此②符合题意;
③∵ABCD,
∴AD=BC,AD∥BC
∴∠DAE=∠BCF
在△ADE和△BCF中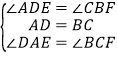
∴△ADE≌△BCF
∴DE=BF,∠DEA=∠BFC
∴∠DEA+∠DEO=180°,∠BFC+∠OFB=180°
∴∠DEO=∠OFB
∴DE∥BF DE=BF
∴四边形DEBF是平行四边形,因此③不符合题意;
④当∠ABE=∠CDF,与③的证明方法一样,可证出四边形DEBF是平行四边形,因此④不符合题意;
因此不能判定四边形DEBF是平行四边形只有②。
故答案为:B
利用平行四边形的性质及判断和全等三角形的性质及判断,逐一判断即可得出答案。


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
【题目】下列各组线段中,能组成三角形的是( )
A. 1cm,2cm,3cm B. 2cm,3cm,4cm
C. 1cm,8cm,4cm D. 4cm,4cm,8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:计算与化简,解分式方程
(1)aa5﹣(2a3)2+(﹣2a2)3
(2)先化简(a﹣ ![]() )
) ![]() ,再求值,其中a=3,b=1
,再求值,其中a=3,b=1
(3)分解因式:(m﹣n)(3m+n)2+(m+3n)2(n﹣m)
(4)解分式方程: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黔东南下司“蓝每谷”以盛产“优质蓝莓”而吸引来自四面八方的游客,某果农今年的蓝莓得到了丰收,为了了解自家蓝莓的质量,随机从种植园中抽取适量蓝莓进行检测,发现在多次重复的抽取检测中“优质蓝莓”出现的频率逐渐稳定在0.7,该果农今年的蓝莓总产量约为800kg,由此估计该果农今年的“优质蓝莓”产量约是kg.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,目前我国每年可利用的淡水资源总量为27500亿米3 , 人均占有淡水量居全世界第110位,因此我们要节约用水,27500亿用科学记数法表示为( )
A.275×104
B.2.75×104
C.2.75×1012
D.27.5×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当点E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )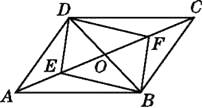
A.OE=OF
B.DF=BE
C.AE=CF
D.∠AEB=∠CFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )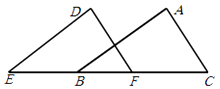
A.AB=DE
B.DF∥AC
C.∠E=∠ABC
D.AB∥DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com