
 在图①所标注的6个角中共有,1对同位角,3对内错角,4对同旁内角,在图②中共有3对同旁内角.
在图①所标注的6个角中共有,1对同位角,3对内错角,4对同旁内角,在图②中共有3对同旁内角. 分析 根据同位角就是:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角,内错角是两个角都在截线的两侧,又分别处在被截的两条直线中间的位置的角,同旁内角是两个角都在截线的同旁,又分别处在被截的两条直线中间位置的角,可得答案.
解答 解:在图①所标注的6个角中∠1与∠4是同位角,∠3与∠6,∠1与∠3,∠4与∠5是内错角,∠2与∠3,∠2与∠4,∠3与∠4,∠5与∠6是同旁内角,故共有1对同位角,3对内错角,4对同旁内角,在图②中∠CAB与∠B,∠B与∠C,∠C与∠CAB是同旁内角,故共有3对同旁内角.
故答案为:1,3,4,3.
点评 本题考查了同位角、内错角、同旁内角,解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
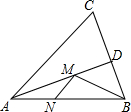 如图,在锐角△ABC中,∠BAC=30°,AB=6,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
如图,在锐角△ABC中,∠BAC=30°,AB=6,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C.
如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com