
 如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C.
如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C.分析 (1)如图1中,设A(x1,0),B(x2,0),由△AOC∽△COB,得$\frac{OA}{CO}$=$\frac{CO}{OB}$,即OC2=OA•OB,因为OC=-c,OA•OB=-x1•x2,x1x2=$\frac{c}{a}$,可得c2=-$\frac{c}{a}$,可得ac=-1.
(2)①如图2中,设AB的中点为K(1,0),D(m,m2-2m-3).根据KD=2,可得方程(m-1)2+(m2-2m-3)2=4,列方程即可.
②如答图3,连接AD、BC.由△AOE∽△COB,得$\frac{OE}{OB}$=$\frac{OA}{OC}$,设A(x1,0),B(x2,0),由题意OC=-c,x1x2=c,求出OE的长即可解决问题.
解答 (1)解:如图1中,设A(x1,0),B(x2,0),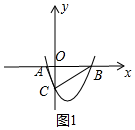
∵△ABC是直角三角形,
∴∠ACB=90°,
∵∠ACO+∠CAO=90°,∠CAB+∠CBO=90°,
∴∠ACO=∠CBO,∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴$\frac{OA}{CO}$=$\frac{CO}{OB}$,
∴OC2=OA•OB,
∵OC=-c,OA•OB=-x1•x2,x1x2=$\frac{c}{a}$,
∴c2=-x1x1,
∴c2=-$\frac{c}{a}$,
∴ac=-1.
(2)①如图2中,设AB的中点为K(1,0),D(m,m2-2m-3).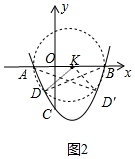
由题意KD=2,
∴(m-1)2+(m2-2m-3)2=4,
∴m2-2m+1+(m2-2m-3)2=4,
∴m2-2m-3+(m2-2m-3)2=0,
∴(m2-2m-3)(1+m2-2m-3)=0,
∴m2-2m-3=0或m2-2m-2=0,
解得m=1+$\sqrt{3}$或1-$\sqrt{3}$或-1或3,(m=-1或m=3不合题意舍弃)
∴D(1-$\sqrt{3}$,-1),D′(1+$\sqrt{3}$,-1).
②证明:如答图3,连接AD、BC.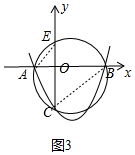
∵∠ADO=∠CBO,∠DAO=∠BCO,
∴△AOE∽△COB,
∴$\frac{OE}{OB}$=$\frac{OA}{OC}$,
设A(x1,0),B(x2,0),
∵已知抛物线y=x2+bx+c(c<0),∴OC=-c,x1x2=c.
∴$\frac{OE}{{x}_{2}}$=$\frac{{x}_{1}}{-c}$,
∴OE=$\frac{-{x}_{1}{x}_{2}}{-c}$=$\frac{-c}{-c}$=1
∴无论b,c取何值,点E均为定点,该定点坐标E(0,1).
点评 本题考查二次函数综合题、圆的有关知识、相似三角形的判定和性质、一元二次方程、根与系数的关系等知识,解题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,(2)①中的解方程是难点,本题考查学生综合应用知识的能力,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
| 摸到黑球的频率$\frac{m}{n}$ | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 | a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
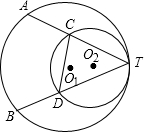 已知:如图,⊙O1与⊙O2内切于点T,⊙O1的弦TA、TB交⊙O2于点C和D,若DC=5,$\frac{TC}{TA}$=$\frac{2}{3}$,求AB的长.
已知:如图,⊙O1与⊙O2内切于点T,⊙O1的弦TA、TB交⊙O2于点C和D,若DC=5,$\frac{TC}{TA}$=$\frac{2}{3}$,求AB的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com