
【题目】如图,抛物线y=ax2+6x+c交x轴于A、B两点,交y轴于点C.直线y=x﹣5经过点B、C.
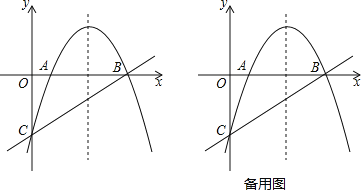
(1)求抛物线的解析式;
(2)过点A作AM⊥BC于点M,过抛物线上一动点P(不与点B、C重合),作直线AM的平行线交直线BC于点Q,若以点A、M、P、Q为顶点的四边形是平行四边形,求点P的横坐标.
【答案】(1)y=-x2+6x-5;(2)点P的横坐标为4或![]() 或
或![]() .
.
【解析】
(1)求出C(0,-5)、点B(5,0),将点A、B的坐标代入二次函数表达式,即可求解;
(2)分点P在直线BC上方、点P在直线BC下方两种情况,分别求解即可.
(1)当x=0时,y=x-5=-5,即点C(0,-5),同理点B(5,0),
将点A、B的坐标代入二次函数表达式得:![]() ,解得:
,解得:![]() ,
,
故抛物线的表达式为:y=-x2+6x-5;
(2)令y=-x2+6x-5=0,解得:x=1或5,即点A(1,0),
∵OB=OC=5,∴∠OCB=∠OBC=45°,
AM=![]() AB=2
AB=2![]() ,
,
以点A、M、P、Q为顶点的四边形是平行四边形,
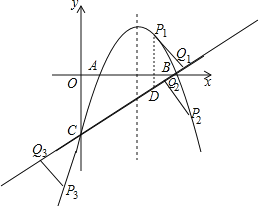
则PQ=AM=2![]() ,PQ⊥BC,
,PQ⊥BC,
如图,作PD⊥x轴交直线BC于D,则∠PDQ=45°,
∴PD=![]() PQ=4,
PQ=4,
设点P(x,-x2+6x-5),则点D(x,x-5),
①当点P在直线BC上方时,
PD=-x2+6x-5-x+5=4,
解得:x=1或4(舍去1);
②点P在直线BC下方时,
PD=-x2+6x-5-x+5=-4,
解得:x=![]() ,
,
故点P的横坐标为4或![]() 或
或![]() .
.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.

(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB=5,AB=6,AB⊥y轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.
(x>0)的图象经过点C,交AB于点D.
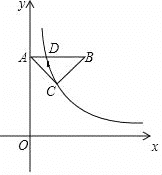
(1)若OA=8,求k的值;
(2)若CB=BD,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .连接
.连接![]() .
.
(1)求抛物线的解析式和点![]() 的坐标;
的坐标;
(2)“若点![]() 为第四象限内抛物线上一动点,点
为第四象限内抛物线上一动点,点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
(3)抛物线的对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出所有点
为等腰三角形?若存在,请直接写出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,E是CD延长线上的一点,BE与AD交于点F,DE=![]() CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
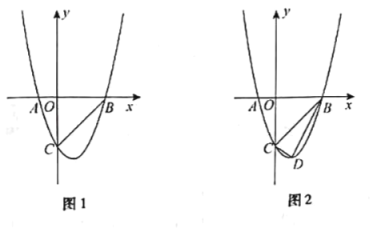
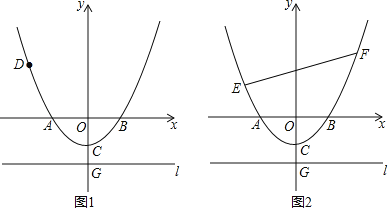
【题目】已知如图1,在以O为原点的平面直角坐标系中,抛物线y=![]() x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1.
x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1.
(1)求抛物线对应的二次函数的解析式;
(2)若D(﹣4,m)为抛物线y=![]() x2+bx+c上一定点,点D到直线l的距离记为d,当d=DO时,求t的值.
x2+bx+c上一定点,点D到直线l的距离记为d,当d=DO时,求t的值.
(3)如图2,若E(﹣4,m)为上述抛物线上一点,在抛物线上是否存在点F,使得△BEF是直角三角形,若存在求出点F的坐标,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.“明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
B.“抛一枚硬币,正面朝上的概率为![]() ”,表示每抛掷两次就有一次正面朝上
”,表示每抛掷两次就有一次正面朝上
C.“抛一枚均匀的正方体骰子,朝上的点数是6的概率为![]() ”,表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的概率稳定在
”,表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的概率稳定在![]() 附近
附近
D.某种彩票的中奖概率为![]() ,买1000张这种彩票一定有一张中奖
,买1000张这种彩票一定有一张中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量![]() (本)与销售单价
(本)与销售单价![]() (元)之间的函数关系式及自变量的取值范围.
(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠![]() 元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求
元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com