练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．请你写出三个大于1的无理数：$\sqrt{2}$，$\sqrt{3}$，π．

    分析 根据无理数是无限不循环小数，可得答案．

    解答 解：写出三个大于1的无理数：$\sqrt{2}$，$\sqrt{3}$，π，
    故答案为：$\sqrt{2}$，$\sqrt{3}$，π．

    点评 此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，$\sqrt{6}$，0.8080080008…（每两个8之间依次多1个0）等形式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

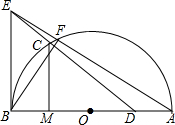    5．如图，在半径为2的⊙O中，AB是直径，C是弧AB的三等分点（∠BOC为锐角），D是OA的中点，BE是⊙O的切线，B为切点，DC的延长线交BE于点E，连接AE，交⊙O于点F．
    （1）求∠BOC的度数；
    （2）作CM⊥AB，垂足为M，连接BF，分别求CM，BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．2016年春节假期期间，我市接待旅游总人数达到9 186 000人次，比去边同期增长1.9%，将9 186 000用科学记数法表示应为（　　）
    A．9186×103B．9.186×105C．9.186×106D．9.186×107

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．已知扇形的弧长为2π，半径为3，则扇形的面积是3π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．实数a在数轴上的位置如图所示，则$\sqrt{（a-2）^{2}}$+$\sqrt{（a-7）^{2}}$化简后为（　　）
    A．5B．-5C．2a-9D．2a+5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．阅读理解：对于二次三项式x2+2ax+a2可以直接用公式法分解为（x+a）2的形式，但对于二次三项式x2+2ax-3a2，就不能直接用公式法了，我们可以在二次三项式x2+2ax-3a2中先加上一项a2，使其成为完全平方式，再减去a2这项，使整个式子的值不变．于是有x2+2ax-3a2=x2+2ax-3a2+a2-a=x2+2ax+a2-a2-3a2=（x+a）2-（2a）2=（x+3a）（x-a）．
    像上面这样把二次三项式分解因式的方法叫做添（拆）项法．
    （1）请用上述方法把x2-4x+3分解因式．
    （2）多项式x2+2x+2有最小值吗？如果有，那么当它有最小值时，x是多少？
    （3）请用上述方法把x4+x2+1分解因式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

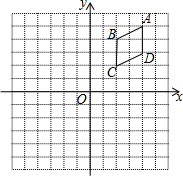    7．如图，在平面直角坐标系中，四边形ABCD的四个顶点坐标分别为A（4，5）、B（2，4）、C（2，2）、D（4，3）．（每个方格的边长均为1个单位长度）
    （1）画出四边形A1B1C1D1，使四边形A1B1C1D1与四边形ABCD关于x轴对称；
    （2）画出四边形A2B2C2D2，使四边形A2B2C2D2与四边形ABCD关于原点成中心对称；
    （3）直接写出四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

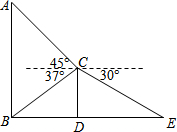    4．某班数学兴趣小组为了测量建筑物AB的高度，他们选取了地面上一点E，测得DE的长度为8.65米，并以建筑物CD的顶端点C为观测点，测得点A的仰角为45°，点B的俯角为37°，点E的俯角为30°．
    （1）求建筑物CD的高度；
    （2）求建筑物AB的高度．
    （参考数据：$\sqrt{3}$≈1.73，sin37°≈$\frac{3}{5}$，cos37°≈$\frac{4}{5}$，tan37°≈$\frac{3}{4}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知关于x的一元二次方程ax2-2（a-1）x+a-1=0有实数根．
    （1）求实数a的取值范围；
    （2）若方程两实数根分别为x1、x2，且满足|x1-x2|=4，求实数a的值．

    查看答案和解析>>

    同步练习册答案