
【题目】已知![]() ,
,![]() ,
,![]() 是等圆,
是等圆,![]() 内接于
内接于![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上.如图,
上.如图,
①以![]() 为圆心,
为圆心,![]() 长为半径作弧交
长为半径作弧交![]() 于点
于点![]() ,连接
,连接![]() ;
;
②以![]() 为圆心,
为圆心,![]() 长为半径作弧交
长为半径作弧交![]() 于点
于点![]() ,连接
,连接![]() ;
;
下面有四个结论:
①![]()
②![]()
③![]()
④![]()
所有正确结论的序号是( ).
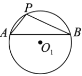
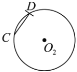
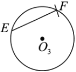
A.①②③④B.①②③C.②④D.②③④
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴的正半轴交于点K,过点
轴的正半轴交于点K,过点![]() 作
作![]() 轴交抛物线于另一点B,点
轴交抛物线于另一点B,点![]() 在
在![]() 轴的负半轴上,连结
轴的负半轴上,连结![]() 交
交![]() 轴于点A,若
轴于点A,若![]() .
.
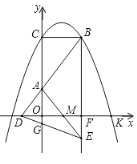
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)当![]() 时,判断点
时,判断点![]() 是否落在抛物线上,并说明理由;
是否落在抛物线上,并说明理由;
(3)过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() 延长
延长![]() 至
至![]() ,使得
,使得![]() 连结
连结![]() 交
交![]() 轴于点
轴于点![]() 连结AE交
连结AE交![]() 轴于点
轴于点![]() 若
若![]() 的面积与
的面积与![]() 的面积之比为
的面积之比为![]() 则求出抛物线的解析式.
则求出抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月15日,我国“两会”落下帷幕.13天时间里,来自各地的5000余名代表、委员聚于国家政治中心,共议国家发展大计.某校初三(3)班张老师为了了解同学们对“两会”知识的知晓情况,进行了一次小测试,测试满分100分.其中
A组同学的测试成绩分别为:91 91 86 93 85 89 89 88 87 91
B组同学的测试成绩分别为:88 97 88 85 86 94 84 83 98 87
根据以上数据,回答下列问题:
(1)完成下表:
组别 | 平均数 | 中位数 | 众数 | 方差 |
A组 | 89 | 89 | b | c |
B组 | 89 | a | 88 | 26.2 |
其中a= ,b= ,c= ,
(2)张老师将B组同学的测试成绩分成四组并绘制成如图所示频数分布直方图(不完整),请补全;
(3)根据以上分析,你认为 组(填“A”或“B”)的同学对今年“两会”知识的知晓情况更好一些,请写出你这样判断的理由(至少写两条):① ② .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形![]() 中,对角线
中,对角线![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,运动速度都是
同时出发,运动速度都是![]() ,点
,点![]() 由
由![]() 向
向![]() 运动;点
运动;点![]() 由
由![]() 向
向![]() 运动,当
运动,当![]() 到达点
到达点![]() 时,
时,![]() ,
,![]() 两点运动停止,设时间为
两点运动停止,设时间为![]() 秒
秒![]() .连接
.连接![]() ,
,![]() ,
,![]() .
.
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)设![]() 的面积为
的面积为![]() ,请写出
,请写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() 的面积是四边形
的面积是四边形![]() 面积的
面积的![]() ;
;
(4)是否存在![]() 值,使得线段
值,使得线段![]() 经过
经过![]() 的中点
的中点![]() ;若存在,求出
;若存在,求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
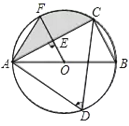
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°,且AB=6,过O点作OE⊥AC,垂足为E.
(1)求OE的长;
(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积.(结果精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
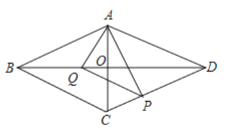
【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,判断正确的有( )
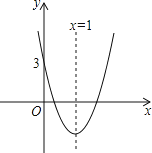
A. ②③④B. ①②③C. ②③D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点O为BC上一点,以点O为圆心、OB的长为半径作圆,交BC于点F,交AB于点D,过点D作⊙O的切线,交AC于点E.
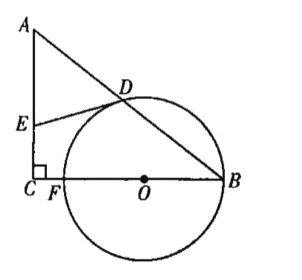
(1)求证:AE=DE;
(2)若![]() ,CF=2,BF=10,求AD的长.
,CF=2,BF=10,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com