
【题目】如图,在△ABC中,∠C=90°,点O为BC上一点,以点O为圆心、OB的长为半径作圆,交BC于点F,交AB于点D,过点D作⊙O的切线,交AC于点E.
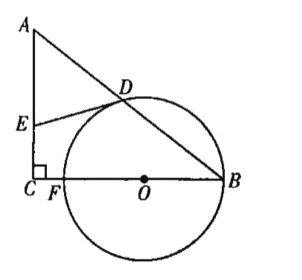
(1)求证:AE=DE;
(2)若![]() ,CF=2,BF=10,求AD的长.
,CF=2,BF=10,求AD的长.
【答案】(1)见解析;(2)AD=7.
【解析】
(1)连接OD,利用切线的性质,得到∠ODE=90°,逐步得到∠A=∠ADE,等角对等边即可证明.
(2)在Rt△ABC中,由题意可得BC=CF+FB=12,AC=9,AB=15;连接DF,由题意可得△FBD∽△ABC,根据对应边成比例即可求解.
(1)证明:如图,连接OD.
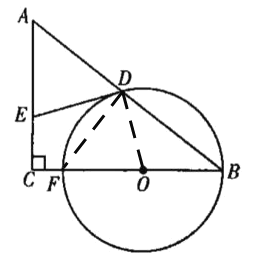
∵DE是⊙O的切线,
∴∠ODE=90°,
∴∠ADE+∠ODB=90°.
∵OD=0B,
∴∠B=∠ODB,
∴∠ADE+∠B=90°
又∵∠A+∠B=180°-∠C=90°,
∴∠A=∠ADE,
∴AE=DE.
(2)在Rt△ABC中:BC=CF+FB=12,![]()
∴AC=9,
∴AB=![]() =15.
=15.
如图,连接DF.
∵BF是⊙O的直径,
∴∠FDB=90°=∠ACB.
又∵∠B=∠B,
∴△FBD∽△ABC,
∴![]()
即![]()
∴BD=8,
∴AD=AB-BD=7.


科目:初中数学 来源: 题型:
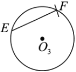
【题目】已知![]() ,
,![]() ,
,![]() 是等圆,
是等圆,![]() 内接于
内接于![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
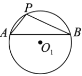
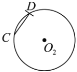
,![]() 上.如图,
上.如图,
①以![]() 为圆心,
为圆心,![]() 长为半径作弧交
长为半径作弧交![]() 于点
于点![]() ,连接
,连接![]() ;
;
②以![]() 为圆心,
为圆心,![]() 长为半径作弧交
长为半径作弧交![]() 于点
于点![]() ,连接
,连接![]() ;
;
下面有四个结论:
①![]()
②![]()
③![]()
④![]()
所有正确结论的序号是( ).
A.①②③④B.①②③C.②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于我国古代著名数学著作《周髀算经》中,为了方便,在本题中,我们把三边的比为3:4:5的三角形称为(3,4,5)型三角形,例如:三边长分别为9,12,15或3![]() ,4
,4![]() ,5
,5![]() 的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
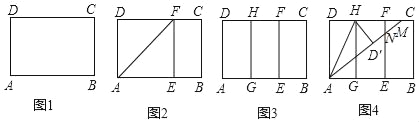
实践操作 如图1,在矩形纸片ABCD中,AD=8cm,AB=12cm.
第一步:如图2,将图1中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图4,将图3中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.
问题解决
(1)请在图2中证明四边形AEFD是正方形.
(2)请在图4中判断NF与ND′的数量关系,并加以证明;
(3)请在图4中证明△AEN(3,4,5)型三角形;
探索发现
(4)在不添加字母的情况下,图4中还有哪些三角形是(3,4,5)型三角形?请找出并直接写出它们的名称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,该商品的进价为每件10元,物价部门限定,每件该商品的销售利润不得超过![]() ,销售过程中发现月销售量
,销售过程中发现月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系满足:当
(元)之间的关系满足:当![]() 时,月销售量为640件;当
时,月销售量为640件;当![]() 时,销售单价每增加1元,月销售量就减少20件.
时,销售单价每增加1元,月销售量就减少20件.
(1)请直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)设该商品的月利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数关系式,并指出当该商品的销售单价定为多少元时,月利润最大,最大月利润是多少.
之间的函数关系式,并指出当该商品的销售单价定为多少元时,月利润最大,最大月利润是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展黄梅戏演唱比赛,组委会将本次比赛的成绩(单位:分)进行整理,并绘制成如下频数分布表和频数分布直方图(不完整).
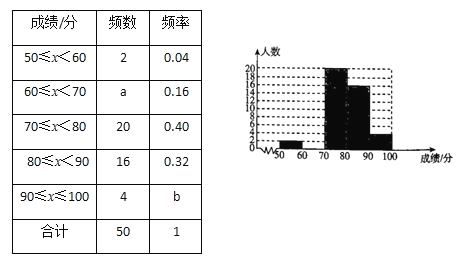
请你根据图表提供的信息,解答下列问题:
(1)求出a,b的值并补全频数分布直方图.
(2)将此次比赛成绩分为三组:A.50≤x<60;B.60≤x<80;C.80≤x≤100.若按照这样的分组方式绘制扇形统计图,则其中C组所在扇形的圆心角的度数是多少?
(3)学校准备从不低于90分的参赛选手中任选2人参加市级黄梅戏演唱比赛,求都取得了95分的小欣和小怡同时被选上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=![]() ;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.

A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
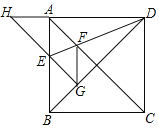
【题目】如图,正方形ABCD的边长为1,AC、BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形;②△HED的面积是1﹣![]() ;③∠AFG=135°;④BC+FG=
;③∠AFG=135°;④BC+FG=![]() .其中正确的结论是_____.(填入正确的序号)
.其中正确的结论是_____.(填入正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
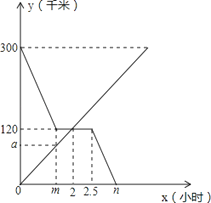
(1)直接写出a,m,n的值;
(2)求出甲车与B地的距离y(千米)与甲车出发时间x(小时)的函数关系式(写出自变量x的取值范围);
(3)当两车相距120千米时,乙车行驶了多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com