
ЁОЬтФПЁПФГжабЇПЊеЙЛЦУЗЯЗбнГЊБШШќЃЌзщЮЏЛсНЋБОДЮБШШќЕФГЩМЈ(ЕЅЮЛЃКЗж)НјааећРэЃЌВЂЛцжЦГЩШчЯТЦЕЪ§ЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМ(ВЛЭъећ)ЃЎ
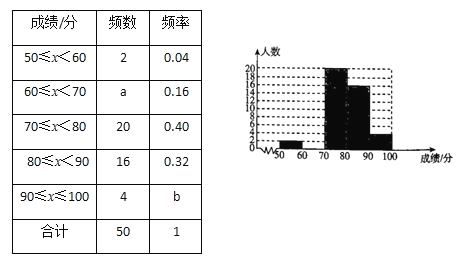
ЧыФуИљОнЭМБэЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓГіaЃЌbЕФжЕВЂВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЎ
ЃЈ2ЃЉНЋДЫДЮБШШќГЩМЈЗжЮЊШ§зщЃКAЃЎ50ЁмxЃМ60ЃЛBЃЎ60ЁмxЃМ80ЃЛCЃЎ80ЁмxЁм100.ШєАДееетбљЕФЗжзщЗНЪНЛцжЦЩШаЮЭГМЦЭМЃЌдђЦфжаCзщЫљдкЩШаЮЕФдВаФНЧЕФЖШЪ§ЪЧЖрЩйЃП
ЃЈ3ЃЉбЇаЃзМБИДгВЛЕЭгк90ЗжЕФВЮШќбЁЪжжаШЮбЁ2ШЫВЮМгЪаМЖЛЦУЗЯЗбнГЊБШШќЃЌЧѓЖМШЁЕУСЫ95ЗжЕФаЁаРКЭаЁтљЭЌЪББЛбЁЩЯЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉa=8ЃЌb=0.08ЃЌЭМаЮМћНтЮіЃЛЃЈ2ЃЉ144ЁуЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦЕЪ§ЗжВМЭМжаУПвЛзщФкЕФЦЕЪ§змКЭЕШгкзмЪ§ОнИіЪ§ЃЌЕУЕНзмШЫЪ§ЃЌдйМЦЫуГіaЕФжЕЃЛИљОнЦЕТЪ=ЦЕЪ§ЁТЪ§ОнзмЪ§МЦЫуbЕФжЕЃЛИљОнaВЙШЋжБЗНЭМЃЛ
ЃЈ2ЃЉИљОндВаФНЧЮЊЃК360ЁуГЫвдАйЗжБШНјааМЦЫуМДПЩЃЛ
ЃЈ3ЃЉЛГіЪїзДЭМЃЌИљОнИХТЪЙЋЪННјааМЦЫуМДПЩЃЎ
ЃЈ1ЃЉa=50ЁС0.16=8ЃЌb=![]() =0.08
=0.08
ВЙШЋЦЕЪ§ЗжВМжБЗНЭМШчгвЃК
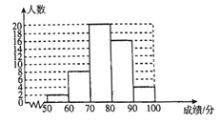
ЃЈ2ЃЉ360ЁуЁС(0.32ЃЋ0.08)=144Ёу
ЙЪCзщЫљдкЩШаЮЕФдВаФНЧЕФЖШЪ§ЮЊ144ЁуЃЎ
ЃЈ3ЃЉгЩЬтвтжЊЃЌВЛЕЭгк90ЗжЕФбЇЩњЙВга4ШЫЃЌЩшетЫФУћбЇЩњЗжБ№ЮЊMЃЌXЃЌAЃЌBЃЌЦфжааЁаРКЭаЁтљЗжБ№гУAЃЌBБэЪОЃЌИљОнЬтвтЃЌЛЪїзДЭМШчЯТЃК
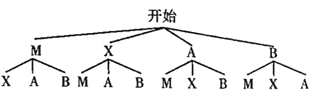
гЩЪїзДЭМПЩжЊЃЌЙВга12жжЕШПЩФмЕФНсЙћЃЌЦфжааЁаРКЭаЁтљЭЌЪББЛбЁЩЯЕФНсЙћга2жжЃЌЙЪаЁаРКЭаЁтљЭЌЪББЛбЁЩЯЕФИХТЪЪЧ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
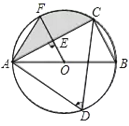
ЁОЬтФПЁПШчЭМЃЌвбжЊABЪЧЁбOЕФжБОЖЃЌЕуCЁЂDдкЁбOЩЯЃЌЁЯDЃН60ЁуЃЌЧвABЃН6ЃЌЙ§OЕузїOEЁЭACЃЌДЙзуЮЊEЃЎ
ЃЈ1ЃЉЧѓOEЕФГЄЃЛ
ЃЈ2ЃЉШєOEЕФбгГЄЯпНЛЁбOгкЕуFЃЌЧѓЯвAFЁЂACКЭЛЁCFЮЇГЩЕФЭМаЮЃЈвѕгАВПЗжЃЉЕФУцЛ§ЃЎЃЈНсЙћОЋШЗЕН0ЃЎ01ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2ЃЋbxЃЋcЃЈaЁй0ЃЉЕФЖдГЦжсЮЊжБЯпxЃНЃ2ЃЌгыxжсЕФвЛИіНЛЕудкЃЈЃ3ЃЌ0ЃЉКЭЃЈЃ4ЃЌ0ЃЉжЎМфЃЌЦфВПЗжЭМЯѓШчЭМЫљЪОЃЎдђЯТСаНсТлЃКЂй4aЃbЃН0ЃЛЂкc<0ЃЛЂлЃ3aЃЋc>0ЃЛЂм4aЃ2b>at2ЃЋbtЃЈtЮЊЪЕЪ§ЃЉЃЛЂнЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧИУХзЮяЯпЩЯЕФЕуЃЌдђy1<y2<y3ЃЎЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
ЪЧИУХзЮяЯпЩЯЕФЕуЃЌдђy1<y2<y3ЃЎЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
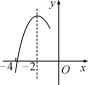
A.4B.3C.2D.1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
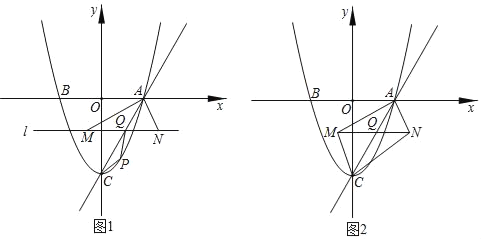
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпyЃНx2Љ3гыxжсНЛгкABСНЕуЃЈЕуAдкЕуBЕФгвВрЃЉЃЌгыyжсНЛгкЕуCЃЌСЌНгACЃЎЕуQЪЧЯпЖЮACЩЯЕФЖЏЕуЃЌЙ§QзїжБЯпlЁЮxжсЃЌжБЯп1гыЁЯBACЕФЦНЗжЯпНЛгкЕуMЃЌгыЁЯCAxЕФЦНЗжЯпНЛгкЕуNЃЎ
ЃЈ1ЃЉPЪЧжБЯпACЯТЗНХзЮяЯпЩЯвЛЖЏЕуЃЌСЌНгPAЃЌPCЃЌЕБЁїPACЕФУцЛ§зюДѓЪБЃЌЧѓPQ+![]() AMЕФзюаЁжЕЃЛ
AMЕФзюаЁжЕЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгMCЃЌNCЃЌЕБЫФБпаЮAMCNЮЊОиаЮЪБЃЌНЋЁїAMNбизХжБЯпACЦНвЦЕУЕНЁїA'M'N'ЃЌБпA'M'ЫљдкЕФжБЯпгыyжсНЛгкDЕуЃЌШєЁїDM'N'ЮЊЕШбќШ§НЧаЮЪБЃЌЧѓODЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
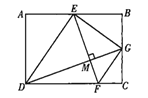
ЁОЬтФПЁПШчЭМЃЌЕуEЪЧОиаЮABCDЕФБпABЕФжаЕуЃЌЕуFЪЧБпCDЩЯвЛЕуЃЌСЌНгEDЃЌEFЃЌEDЦНЗжЁЯAEFЃЌЙ§ЕуDзїDGЁЭEFгкЕуMЃЌНЛBCгкЕуGЃЌСЌНгGEЃЌGFЃЌШєFGЁЮDEЃЌдђ![]() ЕФжЕЪЧ(ЁЁЁЁ)
ЕФжЕЪЧ(ЁЁЁЁ)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯCЃН90ЁуЃЌЕуOЮЊBCЩЯвЛЕуЃЌвдЕуOЮЊдВаФЁЂOBЕФГЄЮЊАыОЖзїдВЃЌНЛBCгкЕуFЃЌНЛABгкЕуDЃЌЙ§ЕуDзїЁбOЕФЧаЯпЃЌНЛACгкЕуEЃЎ
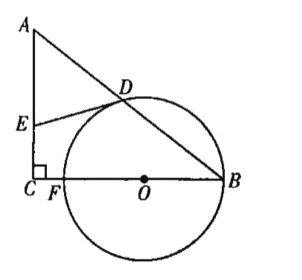
ЃЈ1ЃЉЧѓжЄЃКAEЃНDEЃЛ
ЃЈ2ЃЉШє![]() ЃЌCFЃН2ЃЌBFЃН10ЃЌЧѓADЕФГЄЃЎ
ЃЌCFЃН2ЃЌBFЃН10ЃЌЧѓADЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПВннЎЪЧжжРЯЩйНдвЫЕФЪГЦЗЃЌЩюЪмЪаУёЛЖгЃЎНёФъ3дТЗнЃЌМзЃЌввСНГЌЪаЗжБ№гУ3000дЊвдЯрЭЌЕФНјМлЙКНјжЪСПЯрЭЌЕФВннЎЃЎМзГЌЪаЯњЪлЗНАИЪЧЃКНЋВннЎАДДѓаЁЗжРрАќзАЯњЪлЃЌЦфжаДѓВннЎ400ЧЇПЫЃЌвдНјМлЕФ2БЖМлИёЯњЪлЃЌЪЃЯТЕФаЁВннЎвдИпгкНјМлЕФ10%ЯњЪлЃЎввГЌЪаЯњЪлЗНАИЪЧЃКВЛНЋВннЎАДДѓаЁЗжРрЃЌжБНгАќзАЯњЪлЃЌМлИёАДМзГЌЪаДѓЁЂаЁСНжжВннЎЪлМлЕФЦНОљЪ§ЖЈМлЃЎШєСНГЌЪаНЋВннЎШЋВПЪлЭъЃЌЦфжаМзГЌЪаЛёРћ2100дЊЃЈЦфЫћГЩБОВЛМЦЃЉЃЎ
ЃЈ1ЃЉВннЎНјМлЮЊУПЧЇПЫЖрЩйдЊЃП
ЃЈ2ЃЉввГЌЪаЛёРћЖрЩйдЊЃПВЂБШНЯФФжжЯњЪлЗНЪНИќКЯЫуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() ЕФзѓВрЃЉЃЌЕу
ЕФзѓВрЃЉЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌзїжБЯп
ЃЌзїжБЯп![]() ЃЎЖЏЕу
ЃЎЖЏЕу![]() дк
дк![]() жсЩЯдЫЖЏЃЌЙ§Еу
жсЩЯдЫЖЏЃЌЙ§Еу![]() зї
зї![]() жсЃЌНЛХзЮяЯпгкЕу
жсЃЌНЛХзЮяЯпгкЕу![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЎ
ЃЎ
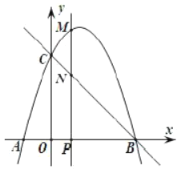
ЃЈ1ЃЉжБНгаДГіХзЮяЯпЕФНтЮіЪН__________КЭжБЯп![]() ЕФНтЮіЪН_________ЃЛ
ЕФНтЮіЪН_________ЃЛ
ЃЈ2ЃЉЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯдЫЖЏЪБЃЌжБНгаДГіЯпЖЮ
ЩЯдЫЖЏЪБЃЌжБНгаДГіЯпЖЮ![]() ГЄЖШЕФзюДѓжЕ_________ЃЛ
ГЄЖШЕФзюДѓжЕ_________ЃЛ
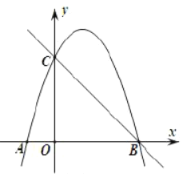
ЃЈ3ЃЉЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯдЫЖЏЪБЃЌШє
ЩЯдЫЖЏЪБЃЌШє![]() ЪЧвд
ЪЧвд![]() ЮЊбќЕФЕШбќжБНЧШ§НЧаЮЪБЃЌЧѓ
ЮЊбќЕФЕШбќжБНЧШ§НЧаЮЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ4ЃЉЕБвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЧѓГі
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЧѓГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=ax2+bx+cЕФЭМЯѓШчЭМЫљЪОЃЌЫќгыxжсЕФСНИіНЛЕуЗжБ№ЮЊЃЈЉ1ЃЌ0ЃЉЃЌЃЈ3ЃЌ0ЃЉЃЎЖдгкЯТСаУќЬтЃКЂйbЉ2a=0ЃЛЂкabcЃМ0ЃЛЂлaЉ2b+4cЃМ0ЃЛЂм8a+cЃО0ЃЎЦфжае§ШЗЕФгаЃЈ ЃЉ
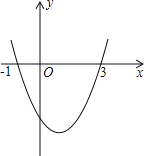
A.3ИіB.2ИіC.1ИіD.0Иі
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com