
����Ŀ���ۺ���ʵ��
�����Ķ� ������ǧ����ǰ���ҹ��ܳ���ѧ���̸߾��������һ��ֱ���۳�һ��ֱ�ǣ���������������ɵ����ģ���ô�Ҿ͵����壬�������������ġ����塱�������������ҹ��Ŵ�������ѧ�����������㾭���У�Ϊ�˷��㣬�ڱ����У����ǰ����ߵı�Ϊ3��4��5�������γ�Ϊ��3��4��5���������Σ����磺���߳��ֱ�Ϊ9��12��15��3![]() ��4
��4![]() ��5
��5![]() �������ξ��ǣ�3��4��5���������Σ��þ���ֽƬ������IJ������������۳��������͵������Σ�
�������ξ��ǣ�3��4��5���������Σ��þ���ֽƬ������IJ������������۳��������͵������Σ�
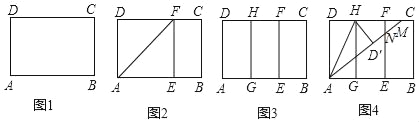
ʵ������ ��ͼ1���ھ���ֽƬABCD�У�AD=8cm��AB=12cm��
��һ������ͼ2����ͼ1�еľ���ֽƬABCD�ع���A��ֱ���۵���ʹ��D����AB�ϵĵ�E�����ۺ�ΪAF������EF�۵���Ȼ���ֽƬչƽ��
�ڶ�������ͼ3����ͼ2�еľ���ֽƬ�ٴ��۵���ʹ��D���F�غϣ��ۺ�ΪGH��Ȼ��չƽ����ȥAF��
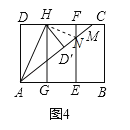
����������ͼ4����ͼ3�еľ���ֽƬ��AH�۵����õ���AD��H������AD���۵����ۺ�ΪAM��AM���ۺ�EF���ڵ�N��Ȼ��չƽ��
������
��1������ͼ2��֤���ı���AEFD�������Σ�
��2������ͼ4���ж�NF��ND���������ϵ��������֤����
��3������ͼ4��֤����AEN��3��4��5���������Σ�
̽������
��4���ڲ�������ĸ������£�ͼ4�л�����Щ�������ǣ�3��4��5���������Σ����ҳ���ֱ��д�����ǵ����ƣ�
���𰸡���1��֤������������2��NF=ND�䣬���ɼ���������3��֤������������4����MFN����MD��H����MDA�ǣ�3��4��5���������Σ�
��������
������1����������������3��4��5���������εĶ���֤�����ɣ�
��2��NF=ND����֤��Rt��HNF��Rt��HND�����ɣ�
��3����������������3��4��5���������εĶ���֤�����ɣ�
��4������AEN�ǣ�3��4��5���������Σ���������AEN���Ƶ������ǣ�3��4��5���������Σ�
����������⣺��1�����ı���ABCD�Ǿ��Σ����D=��DAE=90�������۵�֪��AE=AD����AEF=��D=90�㣬���D=��DAE=��AEF=90�㣬���ı���AEFD�Ǿ��Σ���AE=AD��������AEFD�������Σ�
��2��NF=ND����֤�����£�
����HN�����۵�֪����AD��H=��D=90�㣬HF=HD=HD�䣮
���ı���AEFD�������Σ����EFD=90�㣮
�ߡ�AD��H=90�㣬���HD��N=90�㣮
��Rt��HNF��Rt��HND���У���HN=HN��HF=HD�䣬��Rt��HNF��Rt��HND�䣬��NF=ND�䣮
��3�����ı���AEFD�������Σ���AE=EF=AD=8cm�����۵�֪��AD��=AD=8cm��EN=EF-NF=��8-x���M��
��Rt��AEN�У��ɹ��ɶ����ã�![]() ����
����![]() ����ã�x=2����AN=8+x=10���M����EN=6���M������AN=6��8��10=3��4��5������AEN�ǣ�3��4��5���������Σ�
����ã�x=2����AN=8+x=10���M����EN=6���M������AN=6��8��10=3��4��5������AEN�ǣ�3��4��5���������Σ�
��4��ͼ4�л��С�MFN����MD��H����MDA�ǣ�3��4��5���������Σ�
��CF��AE�����MFN�ס�AEN��
��EN��AE��AN=3��4��5����FN��MF��CN=3��4��5�����MFN�ǣ�3��4��5���������Σ�
ͬ������MD��H����MDA�ǣ�3��4��5���������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��3��15�գ��ҹ������ᡱ�����Ļ.13��ʱ������Ը��ص�5000����������ίԱ���ڹ����������ģ�������ҷ�չ��ƣ�ijУ������3��������ʦΪ���˽�ͬѧ�Ƕԡ����ᡱ֪ʶ��֪�������������һ��С���ԣ���������100�֣�����
A��ͬѧ�IJ��Գɼ��ֱ�Ϊ��91 91 86 93 85 89 89 88 87 91
B��ͬѧ�IJ��Գɼ��ֱ�Ϊ��88 97 88 85 86 94 84 83 98 87
�����������ݣ��ش��������⣺
��1������±���
��� | ƽ���� | ��λ�� | ���� | ���� |
A�� | 89 | 89 | b | c |
B�� | 89 | a | 88 | 26.2 |
����a���� ����b���� ����c���� ����
��2������ʦ��B��ͬѧ�IJ��Գɼ��ֳ����鲢���Ƴ���ͼ��ʾƵ���ֲ�ֱ��ͼ�������������벹ȫ��
��3���������Ϸ���������Ϊ�� ���飨�A����B������ͬѧ�Խ��ꡰ���ᡱ֪ʶ��֪���������һЩ����д���������жϵ����ɣ�����д������������ ������ ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
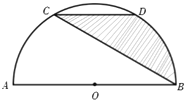
����Ŀ����ͼ��![]() �ǰ�Բ
�ǰ�Բ![]() ��ֱ������
��ֱ������![]() ��
��![]() �ǰ�Բ
�ǰ�Բ![]() �����ȷֵ㣬��
�����ȷֵ㣬��![]() .�ֽ�һ���������ͼ�������������Ӱ����ĸ���Ϊ(����)
.�ֽ�һ���������ͼ�������������Ӱ����ĸ���Ϊ(����)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������߶Գ�����ֱ��x��1����x�����������㣬��y�ύ�������ǣ�0��3������������ƽ��2����λ�õ��µ������߽���ʽ�� y��ax2+bx+c�������ĸ����ۣ���b2��4ac��0����abc��0����4a+2b+c��1����a��b+c��0�У��ж���ȷ���У�������
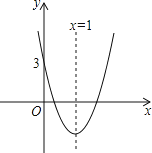
A. �ڢۢ�B. �٢ڢ�C. �ڢ�D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
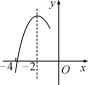
����Ŀ����ͼ��������y��ax2��bx��c��a��0���ĶԳ���Ϊֱ��x����2����x���һ�������ڣ���3��0���ͣ���4��0��֮�䣬�䲿��ͼ����ͼ��ʾ�������н��ۣ���4a��b��0����c<0���ۣ�3a��c>0����4a��2b>at2��bt��tΪʵ�������ݵ�![]() ��
��![]() ��
��![]() �Ǹ��������ϵĵ㣬��y1<y2<y3��������ȷ���۵ĸ����ǣ�������
�Ǹ��������ϵĵ㣬��y1<y2<y3��������ȷ���۵ĸ����ǣ�������
A.4B.3C.2D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
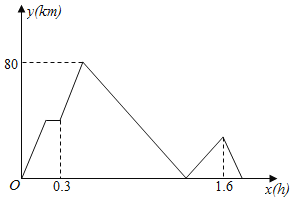
����Ŀ��A��B��վ���330ǧ�ף��ס�����������Aվ��������Bվ���׳��ȳ���������;��Cվͣ��6���ӣ��׳�������Сʱ���ҳ���Aվֱ��Bվ��ֹͣ������֮��ľ���y��ǧ�ף���׳���ʻ��ʱ��x��Сʱ��֮��ĺ���ͼ����ͼ�����ҳ�ǡ���ϼ׳�ʱ����Cվ��______ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
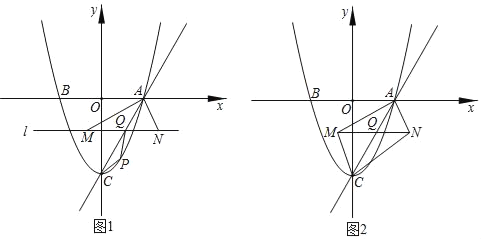
����Ŀ����ͼ1��������y��x2��3��x�ύ��AB���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C������AC����Q���߶�AC�ϵĶ��㣬��Q��ֱ��l��x�ᣬֱ��1���BAC��ƽ���߽��ڵ�M�����CAx��ƽ���߽��ڵ�N��
��1��P��ֱ��AC�·���������һ���㣬����PA��PC������PAC��������ʱ����PQ+![]() AM����Сֵ��
AM����Сֵ��
��2����ͼ2������MC��NC�����ı���AMCNΪ����ʱ������AMN����ֱ��ACƽ�Ƶõ���A'M'N'����A'M'���ڵ�ֱ����y�ύ��D�㣬����DM'N'Ϊ����������ʱ����OD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C��90������OΪBC��һ�㣬�Ե�OΪԲ�ġ�OB�ij�Ϊ�뾶��Բ����BC�ڵ�F����AB�ڵ�D������D����O�����ߣ���AC�ڵ�E��
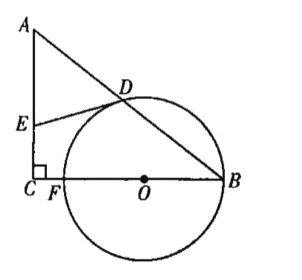
��1����֤��AE��DE��
��2����![]() ��CF��2��BF��10����AD�ij���
��CF��2��BF��10����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ϲ����Ѿ���Ϊ���dz��õ�һ�ֹ��﷽ʽ���ۺ������ر����˹�ע�������������깺��ij����Ʒ�����С����������������������������������ۣ����������������ǵȿ��ܵģ�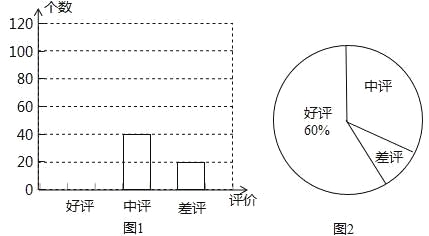
��1��С����һ����������ij����Ʒ��ʾ��������Ϣ������ͳ�ƣ����г���������������ͳ��ͼ������ͼ�����ṩ����Ϣ����������⣺
��С��һ��ͳ���˶��ٸ����ۣ�
���뽫ͼ1����������
�����ͼ2�С���������������Բ�ĽǵĶ�����
��2�����ס��������������ڸ����깺����ͬһ��Ʒ���������б������״ͼ�ķ�������������һ��������������һ�������������ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com