
分析 首先根据题意作出图形,然后可得△OBC是等边三角形,然后由三角函数的性质,求得OH的长,继而求得正六边形的面积.
解答 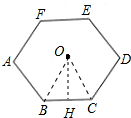 解:如图,连接OB,OC,过点O作OH⊥BC于H,
解:如图,连接OB,OC,过点O作OH⊥BC于H,
∵六边形ABCDEF是正六边形,
∴∠BOC=$\frac{1}{6}$×360°=60°,
∵OB=0C,
∴△OBC是等边三角形,
∴BC=OB=OC=2,
∴它的半径为2,边长为2;
∵在Rt△OBH中,OH=OB•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴边心距是:$\sqrt{3}$;
∴S正六边形ABCDEF=6S△OBC=6×$\frac{1}{2}$×2×$\sqrt{3}$=6$\sqrt{3}$.
故答案为:2,$\sqrt{3}$,6$\sqrt{3}$.
点评 本题考查了圆的内接正六边形的性质、正多边形的内角和、等边三角形的判定与性质以及三角函数等知识.此题难度不大,注意掌握数形结合思想的应用


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售量 | 单价 |
| 不超过100件的部分 | 2.5元/件 |
| 超过100件不超过300件的部分 | 2.2元/件 |
| 超过300件的部分 | 2元/件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-1)(3+x)=5 | B. | x2+$\frac{1}{x}$-$\frac{9}{2}$=0 | C. | y2+2x+4=0 | D. | 4x2=(2x-1)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com