
分析 (1)根据等比数列的定义可得;
(2)由数列中的每一项等于首项乘以公比的序数减一次方可得;
(3)根据定义先求得首项,再根据通项公式即可得;
(4)根据通项公式得$\left\{\begin{array}{l}{{a}_{1}{q}^{2}=12}\\{{a}_{1}{q}^{5}=96}\end{array}\right.$,求得首项和公比,继而根据通项公式可得答案.
解答 解:(1)根据题意知公比q=6÷3=2,第4项是12×2=24,
故答案为:2,24;
(2)根据定义我们可依次写出这个数列的每一项:a1,a1q,a1•q2,a1•q3,….由此可得第n项an=a1•qn-1,
故答案为:a1•qn-1;
(3)根据题意知,第1项为10÷2=5,第4项为5×23=40;
(4)根据题意知$\left\{\begin{array}{l}{{a}_{1}{q}^{2}=12}\\{{a}_{1}{q}^{5}=96}\end{array}\right.$,
∴q3=8,即q=2,
则a1=3,
∴这个等比数列的第10项为3×29=1536.
点评 本题主要考查数字的变化规律,熟练掌握等比数列的定义及其通项公式是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
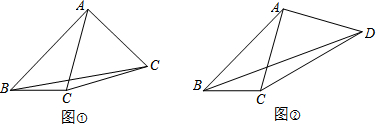
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x+3)=x2+3x | B. | 2n2-mn-n=2n(n-m-1) | ||
| C. | -x2-4y2+4xy=-(x-2y)2 | D. | 2x3-8x=2x(x2-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “明天降雨的概率是75%”表示明天有75%的时间都在降雨 | |
| B. | “抛一枚硬币正面朝上的概率为$\frac{1}{2}$”表示每抛2次就有1次正面朝上 | |
| C. | “抛一枚均匀的正方体骰子,朝上的点数是2的概率为$\frac{1}{6}$”表示随着抛掷次数的增加,“抛出朝上的点数是2”这一事件发生的频率稳定在$\frac{1}{6}$左右 | |
| D. | “彩票中奖的概率为1%”表示买100张彩票肯定会中奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
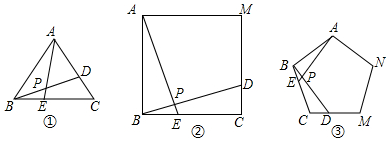
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com