
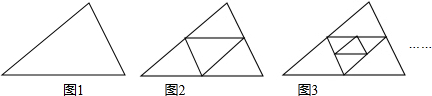
分析 (1)从前三个图形的变化情况找出规律解答即可;
(2)根据代数式的值求出m即可;
(3)把具体数据代入、根据规律进行计算即可.
解答 解:(1)编号为1的图形中有1个三角形,即3×1-2个;
编号为2的图形中有4个互不重叠的三角形,即3×2-2个;
编号为3的图形中有7个互不重叠的三角形,即3×3-2个;
∴编号为n的图形中互不重叠的三角形的个数是3n-2;
(2)由题意得,3m-2=298,
解得,m=100;
(3)S2-S3+S4-S5…-S99+S100
=4-7+10-13…-295+298
=-3×49+298
=151.
点评 本题考查的是规律性:图形的变化类知识,根据图形的特点和变化情况寻找出正确的变化规律是解题的关键,探寻规律要认真观察、仔细思考,善用联想来解决这类问题..


科目:初中数学 来源: 题型:解答题
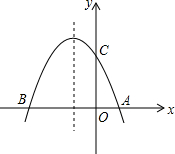 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于C点,且A(1,0),C(0,3),抛物线的对称轴为x=-1.
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于C点,且A(1,0),C(0,3),抛物线的对称轴为x=-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$x=5的解是x=-$\frac{3}{5}$ | B. | 7x=-4的解是x=-$\frac{7}{4}$ | ||
| C. | -x=0的解是x=-1 | D. | $\frac{x}{-10}=0$的解是x=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
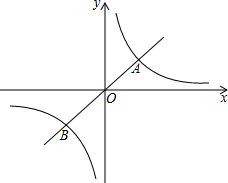 若反比例函数y=$\frac{6}{x}$与正比例函数y=mx的图象相交于点A(a,2)与点B.
若反比例函数y=$\frac{6}{x}$与正比例函数y=mx的图象相交于点A(a,2)与点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | -1 | 0 | 1 | 1.1 | 1.2 | 1.3 |
| ax2+bx+c | -26 | -15 | -2 | -0.59 | 0.84 | 2.29 |
| A. | x<-1 | B. | -1<x<1 | C. | 1.1<x<1.2 | D. | 1.2<x<1.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com