
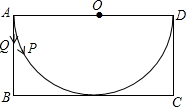
 有一张矩形纸片ABCD,其中AD=4cm,其中AD=4cm,上面有一个以AD为直径的半圆,正好与对边BC相切,如图,动点P、Q分别以每秒1cm的速度从A点出发,P点沿$\widehat{AD}$运动到点D,Q点沿A→B→C→D方向运动.(π取3.14)
有一张矩形纸片ABCD,其中AD=4cm,其中AD=4cm,上面有一个以AD为直径的半圆,正好与对边BC相切,如图,动点P、Q分别以每秒1cm的速度从A点出发,P点沿$\widehat{AD}$运动到点D,Q点沿A→B→C→D方向运动.(π取3.14)分析 (1)根据扇形POD的周长=OP+OD+弧PD的长,弧PD的长=半圆的弧长-弧AP的长,由此即可计算.
(2)点Q运动到BC中点时,点Q运动到BC边上,根据S△ADQ=$\frac{1}{2}$S矩形ABCD即可计算.
解答 解: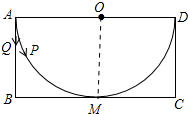 如图设⊙O与BC相切于点M,连接OM,
如图设⊙O与BC相切于点M,连接OM,
∴OM⊥BC,AO=OM=OD=2,
∵四边形ABCD是矩形,
∴∠OAB=∠B=∠OMB=90°,
∴四边形ABMO是矩形,
∵OA=OM,
∴四边形ABMO是正方形,
∴AB=CD=OM=2,
(1)P点运动2秒后,弧AP=2cm,
扇形POD的周长=OP+OD+弧PD=4+(π•2-2)=2+2π≈8.28cm.
(2)∵点Q运动到BC中点时,点Q运动到BC边上,
∴S△ADQ=$\frac{1}{2}$S矩形ABCD=$\frac{1}{2}$×4×2=4.
点评 此题考查了切线的性质,扇形的周长、三角形的面积等知识,理解题意是解题的关键,注意当点P在BC上时,S△ADQ=$\frac{1}{2}$S矩形ABCD,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
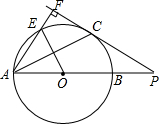 如图,AB是⊙O的直径,点P在AB的延长线上,PC切⊙O于点C,AF⊥PC,垂足是点F,AF交⊙O于点E,PB=2,PC:OE=$\sqrt{3}$:1,
如图,AB是⊙O的直径,点P在AB的延长线上,PC切⊙O于点C,AF⊥PC,垂足是点F,AF交⊙O于点E,PB=2,PC:OE=$\sqrt{3}$:1,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com