
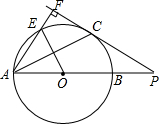
 如图,AB是⊙O的直径,点P在AB的延长线上,PC切⊙O于点C,AF⊥PC,垂足是点F,AF交⊙O于点E,PB=2,PC:OE=$\sqrt{3}$:1,
如图,AB是⊙O的直径,点P在AB的延长线上,PC切⊙O于点C,AF⊥PC,垂足是点F,AF交⊙O于点E,PB=2,PC:OE=$\sqrt{3}$:1,分析 (1)利用切线的性质得OC⊥PC,设PC=$\sqrt{3}$x,OE=x,则OC=OB=x,根据勾股定理得到PO=2x,则x+2=2x,可解得x=2,于是得到PC=2$\sqrt{3}$,OC=2,OP=4,然后证明∠P=∠PAC=30°,从而得到AC=PC=2$\sqrt{3}$;
(2)连结CE,如图,先证明∠FAC=∠OCA=30°,利用含30度的直角三角形三边的关系得到CF=$\frac{1}{2}$AC=$\sqrt{3}$,再证明∠FCE=30°,于是可计算出EF,然后计算CF与EF的乘积.
解答 解:(1)∵PC切⊙O于点C,
∴OC⊥PC,
设PC=$\sqrt{3}$x,OE=x,则OC=OB=x,
在Rt△POC中,PO=$\sqrt{{x}^{2}+(\sqrt{3}x)^{2}}$=2x,
而OB+PB=OP,
∴x+2=2x,解得x=2,
∴PC=2$\sqrt{3}$,OC=2,OP=4,
∴∠P=30°,∠POC=60°,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠POC=∠OAC+∠OCA=60°,
∴∠OAC=∠OCA=30°,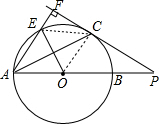
∴∠P=∠PAC,
∴AC=PC=2$\sqrt{3}$;
(2)连结CE,如图,
∵AF⊥PF,OC⊥PF,
∴AF∥OC,
∴∠FAC=∠OCA=30°,
在Rt△AFC中,CF=$\frac{1}{2}$AC=$\sqrt{3}$,
∵∠COF=2∠EAC=60°,
∴△OCE为等边三角形,
∴∠OCE=60°,
∴∠FCE=30°,
在Rt△CEF中,EF=$\frac{\sqrt{3}}{3}$CF=1,
∴CF•EF=$\sqrt{3}$×1=$\sqrt{3}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.解决本题的关键是确定∠P为30°.


科目:初中数学 来源: 题型:选择题
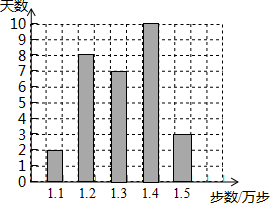 李阿姨是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成如图所示的统计图,在每天所走的步数这组数据中,众数和中位数分别是( )
李阿姨是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成如图所示的统计图,在每天所走的步数这组数据中,众数和中位数分别是( )| A. | 1.2,1.3 | B. | 1.4,1.3 | C. | 1.4,1.35 | D. | 1.3,1.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
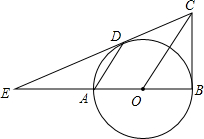 如图,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.
如图,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
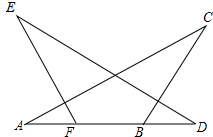 如图,AF=DB,∠A=∠D,添加一个条件,使△ABC≌△DFE,添加的条件不能为( )
如图,AF=DB,∠A=∠D,添加一个条件,使△ABC≌△DFE,添加的条件不能为( )| A. | AC=DE | B. | EF=BC | C. | ∠AFE=∠DBC | D. | ∠E=∠C |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
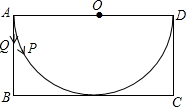 有一张矩形纸片ABCD,其中AD=4cm,其中AD=4cm,上面有一个以AD为直径的半圆,正好与对边BC相切,如图,动点P、Q分别以每秒1cm的速度从A点出发,P点沿$\widehat{AD}$运动到点D,Q点沿A→B→C→D方向运动.(π取3.14)
有一张矩形纸片ABCD,其中AD=4cm,其中AD=4cm,上面有一个以AD为直径的半圆,正好与对边BC相切,如图,动点P、Q分别以每秒1cm的速度从A点出发,P点沿$\widehat{AD}$运动到点D,Q点沿A→B→C→D方向运动.(π取3.14)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com