
【题目】如图所示,两个建筑物AB和CD的水平距离为30m,张明同学住在建筑物AB内10楼P室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.(![]() 取1.73,结果保留整数.)
取1.73,结果保留整数.)
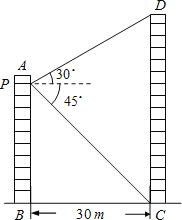
【答案】建筑物CD的高约为47m.
【解析】试题分析:过点P作PE⊥CD于E,则四边形BCEP是矩形,可得PE=BC=30m.在Rt△PDE中,由∠DPE=30°,PE=30m可计算出DE的长度为10![]() m,在Rt△PEC中,由∠EPC=45°,PE=30m可计算出CE的长度为30m,再对DE、CE求和即可.
m,在Rt△PEC中,由∠EPC=45°,PE=30m可计算出CE的长度为30m,再对DE、CE求和即可.
试题解析:
解:过点P作PE⊥CD于E,则四边形BCEP是矩形,
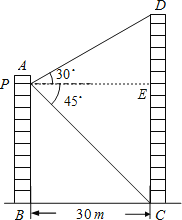
∴PE=BC=30m,
在Rt△PDE中,∵∠DPE=30°,PE=30 m,
∴DE=PE×tan30°=30×![]() =10
=10![]() m.
m.
在Rt△PEC中,∵∠EPC=45°,PE=30 m,
∴CE=PE×tan45°=30×1=30 m,
∴CD=DE+CE=30+10![]() =30+17.3≈47(m).
=30+17.3≈47(m).
答:建筑物CD的高约为47m.


科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从![]() ,
,![]() 两地相向而行,他们距
两地相向而行,他们距![]() 地的距离
地的距离![]() 与时间
与时间![]() 的关系如图所示,下列说法错误的是( )
的关系如图所示,下列说法错误的是( )

A.甲的速度是![]() B.甲出发4.5小时后与乙相遇
B.甲出发4.5小时后与乙相遇
C.乙比甲晚出发2小时D.乙的速度是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠ADC= 度;
(2)当∠C=20°时,判断DE与AC的位置关系,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某品牌轿车以![]() 匀速行驶的耗油情况,进行了试验:该轿车油箱加满后,以
匀速行驶的耗油情况,进行了试验:该轿车油箱加满后,以![]() 的速度匀速行驶,数据记录如下表:
的速度匀速行驶,数据记录如下表:
轿车行驶的路程 | 0 | 100 | 200 | 300 | … |
油箱剩余油量 | 50 | 41 | 32 | 23 | … |
(1)上表反映了哪两个变量之间的关系?自变量、因变量各是什么?
(2)油箱剩余油量![]() (升)与轿车行驶的路程
(升)与轿车行驶的路程![]() (千米)之间的关系式是什么?
(千米)之间的关系式是什么?
(3)若小明将油箱加满后,驾驶该轿车以![]() 的速度匀速从
的速度匀速从![]() 地驶往
地驶往![]() 地,到达
地,到达![]() 地时油箱剩余油量为5升,求两地之间的距离.
地时油箱剩余油量为5升,求两地之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计。图(1)与图(2)是整理数据后绘制的两幅不完整的统计图。以下结论不正确的是( )
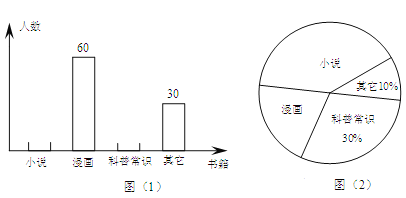
A. 由这两个统计图可知喜欢“科普常识”的学生有90人.
B. 若该年级共有1200名学生,则由这两个统计图可估计喜爱“科普常识”的学生约有360个.
C. 由这两个统计图不能确定喜欢“小说”的人数.
D. 在扇形统计图中,“漫画”所在扇形的圆心角为72°.
查看答案和解析>>
科目:初中数学 来源: 题型:
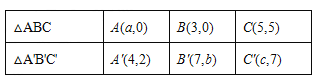
【题目】已知△A'B'C'是由△ABC经过平移得到的,它们的顶点在平面直角坐标系中的坐标如下表所示:
(1)观察表中各对应点坐标的变化,并填空:
a= , b= ,c= ;
(2)在平面直角坐标系中画出△ABC及平移后的△A'B'C';(3)△A'B'C'的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
(1)试求取出的两张卡片数字之和为奇数的概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C表示某旅游景区三个缆车站的位置,线段AB,BC表示连接缆车站的钢缆,已知A,B,C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米,310米,710米,钢缆AB的坡度i1=1∶2,钢缆BC的坡度i2=1∶1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?(注:坡度i是指坡面的铅直高度与水平宽度的比)

【答案】钢缆AC的长度为1 000米.
【解析】试题分析:过点A作AE⊥CC′于点E,交BB′于点F,过点B作BD⊥CC′于点D,分别求出AE、CE,利用勾股定理求解AC即可.
试题解析:过点A作AE⊥CC′于点E,交BB′于点F,过点B作BD⊥CC′于点D,
则△AFB、△BDC、△AEC都是直角三角形,四边形AA′B′F,BB′C′D和BFED都是矩形,
∴BF=BB′-B′F=BB′-AA′=310-110=200,
CD=CC′-C′D=CC′-BB′=710-310=400,
∵i1=1:2,i2=1:1,
∴AF=2BF=400,BD=CD=400,
又∵EF=BD=400,DE=BF=200,
∴AE=AF+EF=800,CE=CD+DE=600,
∴在Rt△AEC中,AC=![]() (米).
(米).
答:钢缆AC的长度是1000米.
考点:解直角三角形的应用-坡度坡角问题.
【题型】解答题
【结束】
24
【题目】如图①,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图②,连接OD交AC于点G,若![]() ,求sinE的值.
,求sinE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前![]() 节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
室内用节能灯 | 40 | 58 |
室外用节能灯 | 50 | 70 |
(1)若该分店共购进节能灯1700盏,问购进的室内用、室外用节能灯各多少盏?
(2)若该分店将进货全部售完后获利要不少于32000元,问至少需要购进多少盏室内用节能灯?
(3)挂职锻炼的大学生村官王祥自酬了4650元在该分店购买这两种类型的节能灯若干盏,分发给村民使用,其中室内用节能灯盏数不少于室内用节能灯盏数的2倍,问王祥最多购买室外用节能灯多少盏?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com