
【题目】目前![]() 节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
室内用节能灯 | 40 | 58 |
室外用节能灯 | 50 | 70 |
(1)若该分店共购进节能灯1700盏,问购进的室内用、室外用节能灯各多少盏?
(2)若该分店将进货全部售完后获利要不少于32000元,问至少需要购进多少盏室内用节能灯?
(3)挂职锻炼的大学生村官王祥自酬了4650元在该分店购买这两种类型的节能灯若干盏,分发给村民使用,其中室内用节能灯盏数不少于室内用节能灯盏数的2倍,问王祥最多购买室外用节能灯多少盏?
科目:初中数学 来源: 题型:
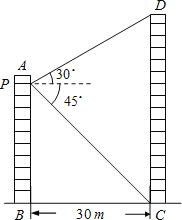
【题目】如图所示,两个建筑物AB和CD的水平距离为30m,张明同学住在建筑物AB内10楼P室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.(![]() 取1.73,结果保留整数.)
取1.73,结果保留整数.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长为1,网格中有一个格点△ABC(即三角形的顶点都在格点上)
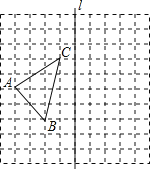
(1)在图中作出△ABC关于直线1对称的△A1B1C1;(要求:A与A1、B与B1、C与C1相对应);
(2)在第(1)问的结果下,连结BB1,CC1,求四边形BB1C1C的面积;
(3)在图中作出△ABC关于点C成中心对称的△A2CB2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
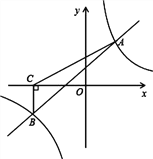
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b≥![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校奖励学生,初一获奖学生中,有一人获奖品3件,其余每人获奖品7件;初二获奖学生中,有一人获奖品4件,其余每人获奖品9件.如果两个年级获奖人数不等,但奖品数目相等,且每个年级奖品数大于50而不超过100,那么两个年级获奖学生共有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BC是直径,∠BAD=120°,AB=AD.
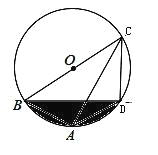
(1)求证:四边形ABCD是等腰梯形;
(2)已知AC=6,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.

(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
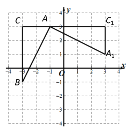
【题目】如图,在平面直角坐标系中,有一Rt△ABC,∠C=90°且A(-1,3)、B(-3,-1)、C(-3,3),已知△A1AC1是由△ABC旋转得到的.若点Q在x轴上,点P在直线AB上,要使以Q、P、A1、C1为顶点的四边形是平行四边形,满足条件的点Q的坐标为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com