
����Ŀ�������Ǵ��ϲ���ּ���һ�������˶�,��������ʱ,��Ҫ����ͬƵ˦������,������˦����ߴ�ʱ,����״�ɽ��ƿ���������,��ͼ��С����С��˦���ӵ���ߴ�ʱ��ʾ��ͼ,���������ӵ���֮��ľ���Ϊ4![]() ,�����ĸ߶�Ϊ1
,�����ĸ߶�Ϊ1![]() ,��С����������λ��Ϊԭ�㽨��ƽ��ֱ������ϵ.
,��С����������λ��Ϊԭ�㽨��ƽ��ֱ������ϵ.
(1)������Ϊ15![]() ��С��վ�����ӵ����·�,�Ҿ�С���������ֵ��Ҳ�1
��С��վ�����ӵ����·�,�Ҿ�С���������ֵ��Ҳ�1![]() ��ʱ,���Ӹպ�ͨ��С���ͷ��,����������Ӧ�������ߵı���ʽ;
��ʱ,���Ӹպ�ͨ��С���ͷ��,����������Ӧ�������ߵı���ʽ;
(2)������Ϊ![]() ��С��Ҳվ�����ӵ����·�.
��С��Ҳվ�����ӵ����·�.
�ٵ�С���ھ�С���������ֵ����1.5![]() ��ʱ,����������С����ͷ��?��˵�����ɣ�
��ʱ,����������С����ͷ��?��˵�����ɣ�
����С����С����������֮���ˮƽ����Ϊ![]() ,Ϊ��֤���Ӳ�����С����ͷ��,��
,Ϊ��֤���Ӳ�����С����ͷ��,��![]() ��ȡֵ��Χ.(�ο�����:
��ȡֵ��Χ.(�ο�����: ![]() ȡ3.16)
ȡ3.16)

���𰸡���1��![]() ����2��������������С����ͷ�����ɼ���������
����2��������������С����ͷ�����ɼ���������![]() .
.
��������
��1����Ϊ�����߹�ԭ�㣬���������ߵĽ���ʽΪ��y=ax2+bx��a��0������С�������ӵ��ֵ����꣨4��0�����Լ�С��ͷ�����꣨1��1.5-1�����룬�õ���Ԫһ�η����飬�ⷽ�����ɣ�
��2�������Ա�����ֵ�������ֵ���ٱȽϱ�ɣ�����y=0.65ʱ������Ա�����ֵ�����ȷ��d��ȡֵ��Χ��
��1����������,����������Ӧ�������ߵı���ʽΪ![]()
��![]() ��
��
�������߾�����![]() �͵�
�͵�![]()
��![]() �����
�����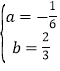
�����Ӷ�Ӧ�������߱���ʽΪ![]()
��2��������������С����ͷ
�������£�
��С���ھ�С���������ֵ����1.5![]() ����
����
��С������λ����ԭ�����Ϊ![]() ��
��
�൱![]() ʱ��
ʱ��![]()
��![]()
������������С����ͷ.
�ڡ�1.65-1=0.65���൱![]() ʱ��
ʱ��![]()
��![]() ����ã�
����ã�![]()
��![]() ȡ3.16
ȡ3.16
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ϊ���ǵ���������˼���ı�������ͼ��һ����������ˮƽ�ĵ����ϣ�����ͷ�·�A���������·�B����ƽ���ڵ����ˮƽ���ϣ�A��B֮��ľ���Ϊ49cm���ֲ��AC��BC��AB�ļнǷֱ�Ϊ45�㣬68�㣮����C������ľ���CDΪ28cm����������E�����B�ľ���BEΪ5cm�����E������ľ��룮���������һλС�����ο����ݣ�sin68���0.93��cos68���0.37��tan68���2.50����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
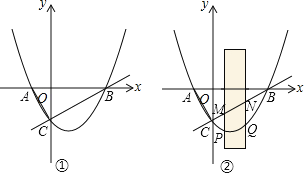
����Ŀ����ͼ�٣�ֱ��y��![]() ��x�ᡢy��ֱ��ڵ�B��C��������y��
��x�ᡢy��ֱ��ڵ�B��C��������y��![]() ��B��C���㣬����x�����һ������Ϊ��A������AC��
��B��C���㣬����x�����һ������Ϊ��A������AC��
��1���������ߵĽ���ʽ��
��2�������������Ƿ���ڵ�D�����A���غϣ���ʹ��S��DBC��S��ABC�������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
��3���п���Ϊ2�������㹻���ľ��Σ���Ӱ���֣���x�᷽��ƽ�ƣ���y��ƽ�е�һ��Ա߽��������ڵ�P�͵�Q����ֱ��CB�ڵ�M�͵�N���ھ���ƽ�ƹ����У����Ե�P��Q��M��NΪ������ı�����ƽ���ı���ʱ�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����۲�������Щ��ʽ,������㷢�ֵĹ���,�����������:

��1�������
��ʽ�� ��
��ʽ�� ��
��2��������ʽ�Ĺ��ɿ��������ָ���Ϊ:����������������ƽ�����ܱ�8������,������������������ֱ�Ϊ![]() ��
��![]() (
(![]() Ϊ����),��˵����������dz�����;
Ϊ����),��˵����������dz�����;
(3)����Ϊ����������ż����ƽ�����ܱ�8���������˵���Ƿ�Ҳ������?��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
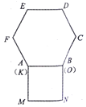
����Ŀ����֪������![]() ����������
���������� ![]() �߳���Ϊ1,��ͼ��ʾ,�������η���������������,ʹ
�߳���Ϊ1,��ͼ��ʾ,�������η���������������,ʹ![]() ����
����![]() ���غ�,�����в�����������������������������Ƶ�
���غ�,�����в�����������������������������Ƶ�![]() ��ʱ����ת,ʹ
��ʱ����ת,ʹ![]() ����
����![]() ���غ�,��ɵ�һ����ת���Ƶ�
���غ�,��ɵ�һ����ת���Ƶ�![]() ��ʱ����ת,ʹ
��ʱ����ת,ʹ![]() ����
����![]() ���غ�,��ɵڶ�����ת����ʱ��
���غ�,��ɵڶ�����ת����ʱ��![]() ����·���ij�Ϊ_________:�����˷�ʽ��ת,���������,�����������,��
����·���ij�Ϊ_________:�����˷�ʽ��ת,���������,�����������,��![]() ֮���������ֵ��____��
֮���������ֵ��____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
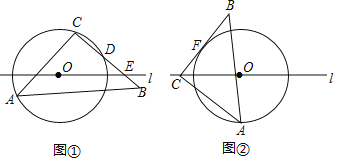
����Ŀ����֪����ABC�У���ACB=90����AC=BC=8����A�ڰ뾶Ϊ5�ġ�O�ϣ���O��ֱ��l�ϣ�
(1)��ͼ�٣�����O������C����BC�ڵ�D����CD�ij���
(2)��(1)�������£���BC�߽�l�ڵ�E��OE=2![]() ����BE�ij���
����BE�ij���
(3)��ͼ�ڣ���ֱ��l��������C��BC�ǡ�O �����ߣ�FΪ�е㣬��CF�ij�Ϊ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֪ʶ����
��a��0��x��0ʱ����Ϊ��![]() ��
��![]() ��2��0������x��2
��2��0������x��2![]() +
+![]() ��0���Ӷ�x+
��0���Ӷ�x+![]() ����x=
����x=![]() ʱȡ�Ⱥţ���
ʱȡ�Ⱥţ���
�躯��y=x+![]() ��a��0��x��0�������������ۿ�֪����x=
��a��0��x��0�������������ۿ�֪����x=![]() ʱ���ú�������СֵΪ2
ʱ���ú�������СֵΪ2![]() ��
��
Ӧ�þ���
��֪����Ϊy1=x��x��0���뺯��y2=![]() ��x��0������x=
��x��0������x=![]() =2ʱ��y1+y2=x+
=2ʱ��y1+y2=x+![]() ����СֵΪ2
����СֵΪ2![]() =4��
=4��
�������
��1����֪����Ϊy1=x+3��x����3���뺯��y2=��x+3��2+9��x����3������xȡ��ֵʱ��![]() ����Сֵ����Сֵ�Ƕ��٣�
����Сֵ����Сֵ�Ƕ��٣�
��2����֪ij�豸����ʹ�óɱ��������������֣�һ���豸�İ�װ���Է��ã���490Ԫ�������豸������ʹ�÷��ã�ÿ��200Ԫ�������豸���۾ɷ��ã�����ʹ��������ƽ�������ȣ�����ϵ��Ϊ0.001��������豸������ʹ������Ϊx�죬��xȡ��ֵʱ�����豸ƽ��ÿ������ʹ�óɱ���ͣ�����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AB=20cm��AD=30cm����ABC=60������Q�ӵ�B������BA���A�����˶����ٶ�Ϊ2cm/s��ͬʱ����P�ӵ�D������DC���C�����˶����ٶ�Ϊ3cm/s������Pֹͣ�˶�ʱ����QҲ��ֹ֮ͣ�˶�������P��PM��AD��AD�ڵ�M������PQ��QM�����˶���ʱ��Ϊts��0��t��6����
��1����PQ��PMʱ����t��ֵ��
��2������PQM�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��t��ʹ����PQM�������ABCD�����![]() �������ڣ������Ӧt��ֵ���������ڣ���˵�����ɣ�
�������ڣ������Ӧt��ֵ���������ڣ���˵�����ɣ�
��4������M��MN��AB��BC�ڵ�N���Ƿ����ijһʱ��t��ʹ��P���߶�MN�Ĵ�ֱƽ�����ϣ������ڣ������Ӧt��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽��
��ͼ��������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
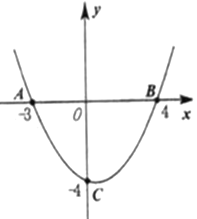
��1���������߽���ʽ��
��2�������߶Գ����ϴ���һ��![]() ������
������![]() ��
��![]() ����
����![]() ֵ���ʱ�����H���꣺
ֵ���ʱ�����H���꣺
��3�����������ϴ���һ��![]() ��
��![]() ����
����![]() ʱ�����
ʱ�����![]() ���꣺
���꣺
��4������M��![]() ƽ�����ϵ�һ�㣬��
ƽ�����ϵ�һ�㣬��![]() ��ƽ����һ�㣬����
��ƽ����һ�㣬����![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����Ǿ��Σ���ֱ��д����
Ϊ������ı����Ǿ��Σ���ֱ��д����![]() ����.
����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com