
【题目】如图,认真观察下面这些算式,并结合你发现的规律,完成下列问题:

(1)请写出:
算式⑤ ;
算式⑥ ;
(2)上述算式的规律可以用文字概括为:“两个连续奇数的平方差能被8整除”,如果设两个连续奇数分别为![]() 和
和![]() (
(![]() 为整数),请说明这个规律是成立的;
为整数),请说明这个规律是成立的;
(3)你认为“两个连续偶数的平方差能被8整除”这个说法是否也成立呢?请说明理由.
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x![]() k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
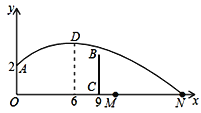
A. 球不会过网 B. 球会过球网但不会出界
C. 球会过球网并会出界 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇中学教学楼对面是一座小山,去年“联通”公司在山顶上建了座通讯铁塔.甲、乙两位同学想测出铁塔的高度,他们用测角器作了如下操作:甲在教学楼顶A处测得塔尖M的仰角为α,塔座N的仰角为β;乙在一楼B处只能望到塔尖M,测得仰角为θ(望不到底座),他们知道楼高AB=20m,通过查表得:tanα=0.5723,tanβ=0.2191,tanθ=0.7489;请你根据这几个数据,结合图形推算出铁塔高度MN的值.
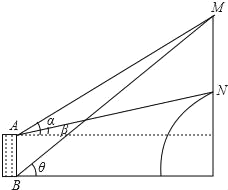
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□![]() 的对角线
的对角线![]() 相交于点
相交于点![]() ,且AE∥BD,BE∥AC,OE = CD.
,且AE∥BD,BE∥AC,OE = CD.
(1)求证:四边形ABCD是菱形;
(2)若AD = 2,则当四边形ABCD的形状是_______________时,四边形![]() 的面积取得最大值是_________________.
的面积取得最大值是_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 和
和![]() ,给出如下定义:若
,给出如下定义:若![]() 上存在一点
上存在一点![]() 不与
不与![]() 重合,使点
重合,使点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在
在![]() 上,则称
上,则称![]() 为
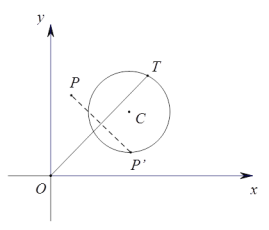
为![]() 的反射点.下图为
的反射点.下图为![]() 的反射点
的反射点![]() 的示意图.
的示意图.
(1)已知点![]() 的坐标为
的坐标为![]() ,
,![]() 的半径为
的半径为![]() ,
,
①在点![]() ,
,![]() ,
,![]() 中,
中,![]() 的反射点是____________;
的反射点是____________;
②点![]() 在直线
在直线![]() 上,若
上,若![]() 为
为![]() 的反射点,求点
的反射点,求点![]() 的横坐标的取值范围;
的横坐标的取值范围;
(2)![]() 的圆心在
的圆心在![]() 轴上,半径为
轴上,半径为![]() ,
,![]() 轴上存在点
轴上存在点![]() 是
是![]() 的反射点,直接写出圆心
的反射点,直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科普小组有5名成员,身高(单位:cm)分别为:160,165,170,163,172,把身高160 cm的成员替换成一位165 cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是( )
A.平均数变小,方差变小B.平均数变大,方差变大
C.平均数变大,方差不变D.平均数变大,方差变小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跳绳是大家喜闻乐见的一项体育运动,集体跳绳时,需要两人同频甩动绳子,当绳子甩到最高处时,其形状可近似看作抛物线,下图是小明和小亮甩绳子到最高处时的示意图,两人拿绳子的手之间的距离为4![]() ,离地面的高度为1
,离地面的高度为1![]() ,以小明的手所在位置为原点建立平面直角坐标系.
,以小明的手所在位置为原点建立平面直角坐标系.
(1)当身高为15![]() 的小红站在绳子的正下方,且距小明拿绳子手的右侧1
的小红站在绳子的正下方,且距小明拿绳子手的右侧1![]() 处时,绳子刚好通过小红的头顶,求绳子所对应的抛物线的表达式;
处时,绳子刚好通过小红的头顶,求绳子所对应的抛物线的表达式;
(2)若身高为![]() 的小丽也站在绳子的正下方.
的小丽也站在绳子的正下方.
①当小丽在距小亮拿绳子手的左侧1.5![]() 处时,绳子能碰到小丽的头吗?请说明理由;
处时,绳子能碰到小丽的头吗?请说明理由;
②设小丽与小亮拿绳子手之间的水平距离为![]() ,为保证绳子不碰到小丽的头顶,求
,为保证绳子不碰到小丽的头顶,求![]() 的取值范围.(参考数据:
的取值范围.(参考数据: ![]() 取3.16)
取3.16)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,![]() ,DE⊥BC,垂足为E.
,DE⊥BC,垂足为E.

(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若CE=1,AC=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
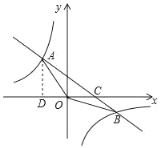
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (n≠0)的图象交于第二、四象限内的A、B两点与x轴交于点C,点B坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=
(n≠0)的图象交于第二、四象限内的A、B两点与x轴交于点C,点B坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=![]()
(1)求该反比例函数和一次函数的解析式;
(2)连接OB,求S△AOC﹣S△BOC的值;
(3)点E是x轴上一点,且△AOE是等腰三角形请直接写出满足条件的E点的个数(写出个数即可,不必求出E点坐标).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com