
分析 (1)利用衬衣平均每天售出的件数×每件盈利=每天销售这种衬衣利润直接求解即可;
(2)利用衬衣平均每天售出的件数×每件盈利=每天销售这种衬衣利润列出方程解答即可;
(3)同样列出方程,若方程有实数根则可以,否则不可以.
解答 解:(1)设每件衬衫应降价x元.
根据题意,得总利润y=(50-x)(20+2x)
令x=5,得到y=45×30=1350元,
答:降价5元可以盈利1350元;
(2)令y=(50-x)(20+2x)=1600
整理,得x2-40x+300=0
解得x1=10,x2=30.
∵“扩大销售量,减少库存”,
∴x1=10应略去,
∴x=30.
答:每件衬衫应降价30元;
(3)令y=(50-x)(20+2x)=2000,
整理,得x2-40x+500=0
∵△=1600-4×500<0,
∴商场平均每天不可能盈利2000元.
点评 此题主要考查了一元二次方程的应用,利用基本数量关系:平均每天售出的件数×每件盈利=每天销售的利润是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
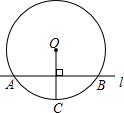 如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )
如图,⊙O的半径OC=10cm,直线AB⊥OC,垂足为H,且交⊙O于A、B两点,AB=12cm,则沿OC直线AB向下平移与⊙O相切,则平移距离为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com