
【题目】如图,在正方形网格上有一个△DEF .
①作△DEF关于直线HG的轴对称图形;
②作△DEF的EF边上的高;
③若网格上的最小正方形边长为1,求△DEF的面积.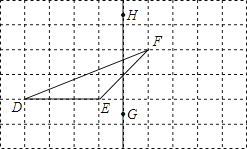
【答案】【解答】①如图所示,△D′E′F′即为所求作的△DEF关于直线HG的轴对称图形;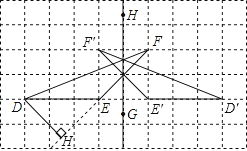
②如图所示,DH为EF边上的高线;
③△DEF的面积![]() .
.
【解析】【分析①根据网格结构找出点D、E、F关于直线HG的对称点D′、E′、F′的位置,然后顺次连接即可;
②根据网格结构以及EF的位置,过点D作小正方形的对角线,与FE的延长线相交于H , DH即为所求作的高线;
③DE为底边,点F到DE的距离为高,根据三角形的面积公式列式进行计算即可得解.
【考点精析】通过灵活运用轴对称图形,掌握两个完全一样的图形关于某条直线对折,如果两边能够完全重合,我们就说这两个图形成轴对称,这条直线就对称轴即可以解答此题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′ , 连接AB′,并有AB′=3,则∠A′的度数为( )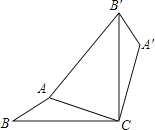
A.125°
B.130°
C.135°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明过程. 如图,在△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,说明ED=EF.
解:∵∠DEC=∠B+∠BDE (),
又∵∠DEF=∠B(已知),
∴∠=∠(等式性质).
在△EBD与△FCE中,
∠=∠(已证),
=(已知),
∠B=∠C(已知),
∴△EBD≌△FCE().
∴ED=EF ().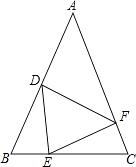
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习中,小明发现:当a=-1,0,1时,a2-8a+20的值都是正数,于是小明猜想:当a为任意整数时,a2-8a+20的值都是正数,小明的猜想正确吗?简要说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),将两块直角三角尺的直角顶点C叠放在一起,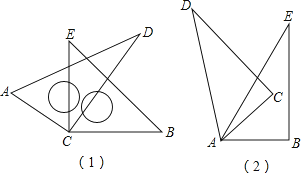
(1)若∠DCE=25°,∠ACB=?;若∠ACB=150°,则∠DCE=?;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com