
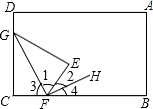
如图,将长方形纸片 ABCD 的角 C 沿着 GF 折叠(点 F 在 BC 上,不与 B,C 重合),使点 C 落 在长方形内部点 E 处,若 FH 平分∠BFE,则∠GFH 的度数是 .

90°【考点】角的计算;翻折变换(折叠问题).
【分析】首先根据折叠方法可得∠1=∠3= 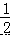 ∠CFE,再根据角平分线性质可知:∠2=∠4,由图形可 知∠1+∠2+∠3+∠4=180°,故∠1+∠2=90°,进而得到∠GFH 的度数.
∠CFE,再根据角平分线性质可知:∠2=∠4,由图形可 知∠1+∠2+∠3+∠4=180°,故∠1+∠2=90°,进而得到∠GFH 的度数.
【解答】解:∵△GFE 是由△GFC 沿 GF 折叠,
∴∠1=∠3= 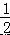 ∠CFE,
∠CFE,
∵FH 平分∠BFE,
∴∠2=∠4= 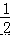 ∠EFB,
∠EFB,
∵∠1+∠2+∠3+∠4=180°,
∴∠1+∠2=90°,
即:∠GFH=90°. 故答案为:90°.
【点评】此题主要考查了翻折变换以及角平分线的性质,解决问题的关键是根据翻折的方法得到∠1 和∠3 的关系,根据角平分线的性质得到∠2 和∠4 的关系.


科目:初中数学 来源: 题型:
如图,数轴上有 A,B,C,D 四个点,其中到原点距离相等的两个点是( )
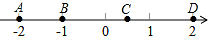
A.点 B 与点 D B.点 A 与点 C C.点 A 与点 D D.点 B 与点 C
查看答案和解析>>
科目:初中数学 来源: 题型:
某数学兴趣小组再用黑色围棋进行摆放图案的游戏中,小雨同学现已摆放了如下的图案,请根 据图中的信息完成下列的问题.
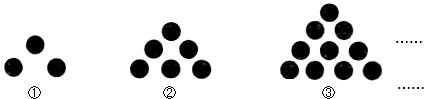
(1)填写下表:
| 图形编号 | ① | ② | ③ | … | … |
| 图中棋子的总数 | 3 | 6 | 10 | … | … |
第 50 个图形中棋子为 1326 颗围棋;
小雨同学如果继续摆放下去,那么第 n 个图案就要用 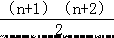 颗围棋;
颗围棋;
(3)如果小雨同学手上刚好有 90 颗围棋子,那么他按照这种规律从第①个图案摆放下去,是否可
以摆放成完整的图案后刚好 90 颗围棋子一颗不剩?如果可以,那么刚好摆放完成几个完整的图案? 如果不行,那么最多可以摆放多少个完整图案,还剩余几颗围棋子?(只答结果,不说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点 C 为线段 AB 上一点,CB=a,D、E 两点分别为 AC、AB 的中点,则线段 DE 的长为
 ( )(用含 a 的代数式表示)
( )(用含 a 的代数式表示)
A. a B. a C. a D. 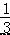 a
a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com