
某数学兴趣小组再用黑色围棋进行摆放图案的游戏中,小雨同学现已摆放了如下的图案,请根 据图中的信息完成下列的问题.
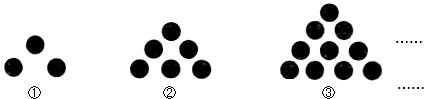
(1)填写下表:
| 图形编号 | ① | ② | ③ | … | … |
| 图中棋子的总数 | 3 | 6 | 10 | … | … |
第 50 个图形中棋子为 1326 颗围棋;
小雨同学如果继续摆放下去,那么第 n 个图案就要用 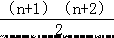 颗围棋;
颗围棋;
(3)如果小雨同学手上刚好有 90 颗围棋子,那么他按照这种规律从第①个图案摆放下去,是否可
以摆放成完整的图案后刚好 90 颗围棋子一颗不剩?如果可以,那么刚好摆放完成几个完整的图案? 如果不行,那么最多可以摆放多少个完整图案,还剩余几颗围棋子?(只答结果,不说明理由)
【考点】规律型:图形的变化类.
【分析】(1)图①可看作 1+2,图②可看作 1+2+3,图③可看作 1+2+3+4; 根据(1)的规律,图 n 可看作 1+2+3+…+(n+1),在按照自然数求和的公式求解;
(3)根据的公式,从图①到图⑥共需围棋数为 3+6+10+15+21+28=83,剩下 7 个棋子,不够了.
【解答】解:根据图形的规律可知: 第①个图案中用了 1+2=3 颗围棋;
第②个图案中用了 1+2+3=6 颗围棋;
第③个图案中用了 1+2+3+4=10 颗围棋;
…;
第 n 个图案中用了 1+2+3+…+(n+1)=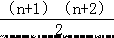 颗围棋. 故答案为:
颗围棋. 故答案为:
(1)在第②个图案中用了 6 颗围棋,在第③个图案中用了 10 颗围棋,在第 50 个图案中,用了 1326
颗围棋,.
小雨同学如果继续摆放下去,那么第 n 个图案就要用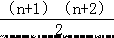 颗围棋.
颗围棋.
(3)不可以,刚好摆放完成 6 个完整图案,还剩下 7 个棋子.
【点评】本题是对图形变化规律的考查,主要考查学生观察问题,归纳总结规律的能力.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
如图,直线 AB 与 x 轴交于点 A(1,0),与 y 轴交于点 B(0,﹣2).
(1)求直线 AB 的解析式;
若直线 AB 上的点 C 在第一象限,且 S△BOC=2,求点 C 的坐标.
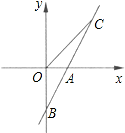
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将长方形纸片 ABCD 的角 C 沿着 GF 折叠(点 F 在 BC 上,不与 B,C 重合),使点 C 落 在长方形内部点 E 处,若 FH 平分∠BFE,则∠GFH 的度数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
某商店规定:超过 15000 元的物品可以采用分期付款方式付款,顾客可以先付 3000 元,以后每
月付 1500 元.王叔叔想用分期付款的形式购买价值 21000 元的物品,他需要用多长时间才能付清全 部货款?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com