练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．求证：
    （1）对角线互相垂直的平行四边形是菱形；
    （2）四条边相等的四边形是菱形．

    分析 （1）首先要写已知，求证．接下来根据菱形的定义证明．
    （2）同上略．

    解答 （1）已知如图1中，四边形ABCD是平行四边形，AC⊥BD，求证：四边形ABCD是菱形．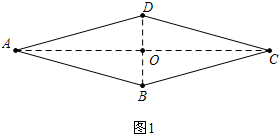
    证明：∵四边形ABCD是平行四边形，
    ∴AO=OC，
    ∵BD⊥AC，
    ∴DA=DC（线段的垂直平分线的性质），
    ∴四边形ABCD是菱形（邻边相等的平行四边形是菱形）．
    （2）已知如图2中，四边形ABCD中，AB=BC=CD=AC，求证四边形ABCD是菱形．
    证明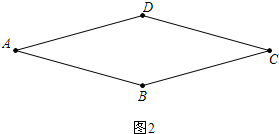：∵AD=BC，AB=CD
    ∴四边形ABCD是平行四边形（对边相等的四边形是平行四边形），
    ∵AD=AB，
    ∴四边形ABCD是菱形（邻边相等的平行四边形是菱形）．

    点评 本题考查菱形的判定，注意点是文字题目首先要写已知、求证，定理证明必须根据菱形定义去证明，记住菱形的定义是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    7．如图，在射线OA，OB上分别截取OA1=OB1，连接A1B1，在B1A1，B1B上分别截取B1A2=B1B2，连接A2B2，…按此规律作下去，若∠A1B1O=α，则∠A10B10O=（　　）
    A．$\frac{α}{{{2^{10}}}}$B．$\frac{α}{2^9}$C．$\frac{α}{{2{0^{\;}}}}$D．$\frac{α}{18}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：
    （1）$-\frac{1}{3}+\frac{1}{4}$
    （2）$-{1^2}+50÷{2^3}×（-\frac{1}{5}）+\frac{1}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．张老师驾车从家出发到植物园赏花，匀速行驶一段时间后，途中遇到堵车原地等待一会儿，然后加速行驶，到达植物园，参观结束后，张老师驾车一路匀速返回，其中x表示汽车从家出发后所用时间，y表示车离家的距离，下面能反映y与x的函数关系式的大致图象是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，已知AD是△ABC的中线，AM⊥AB，AM=AB，AN⊥AC，AN=AC．求证：MN=2AD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

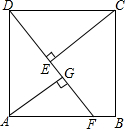    2．如图，正方形ABCD中，F为AB边上一点，过点A，C分别作DF的垂线，垂足为G和E，若AG=3，EG=1，则BF的长为$\frac{5}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．能判断四边形ABCD是平行四边形的条件：∠A：∠B：∠C：∠D的值为（　　）
    A．1：2：3：4B．1：4：2：3C．1：2：2：1D．3：2：3：2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．当m分别取何值时关于x的方程（m-1）x2+（2m-1）x+m-1=0：
    （1）有两个不相等的实数根；
    （2）有两个相等的实数根；
    （3）有两个实数根；
    （4）有一个实数根；
    （5）有实数根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，在△ABC中，AB=AC，AD⊥BD，AE⊥CE，且AD=AE，BD和CE交于点O，请说明OB=OC的理由．

    查看答案和解析>>

    同步练习册答案