
【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)
【答案】解:过点D作DH⊥BC于点M,如图所示: 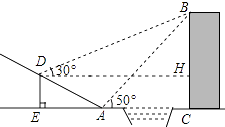
则四边形DHCE是矩形,DH=EC,DE=HC,
设建筑物BC的高度为xm,则BH=(x﹣5)m,
在Rt△DHB中,∠BDH=30°,
∴DH= ![]() (x﹣5),AC=EC﹣EA=
(x﹣5),AC=EC﹣EA= ![]() (x﹣5)﹣10,
(x﹣5)﹣10,
在Rt△ACB中,∠BAC=50°,tan∠BAC= ![]() ,
,
∴x=tan50°[ ![]() (x﹣5)],
(x﹣5)],
解得:x≈21,
答:建筑物BC的高约为21m.
【解析】利用三角函数测物体的高,由四边形DHCE是矩形,得到DH=EC,DE=HC,在Rt△DHB中,∠BDH=30°,得到DH,在Rt△ACB中,∠BAC=50°,由三角函数值求出tan∠BAC的值,得到建筑物BC的高.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】如图1,点![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 是直线
是直线![]() 上一点,且MN//PQ.
上一点,且MN//PQ.![]() 和
和![]() 的平分线交于点
的平分线交于点![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作直线交
作直线交![]() 于点
于点![]() (不与点
(不与点![]() 重合),交
重合),交![]() 于点E,
于点E,
①若点![]() 在点
在点![]() 的右侧,如图2,求证:
的右侧,如图2,求证:![]() ;
;
②若点![]() 在点
在点![]() 的左侧,则线段
的左侧,则线段![]() 、
、![]() 、
、![]() 有何数量关系?直接写出结论,不说理由.
有何数量关系?直接写出结论,不说理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张卡片(形状、大小、颜色、质地都相等),正面分别写上整式x2+1,﹣x2﹣2,3.将这三张卡片背面向上洗匀,从中任意抽取一张卡片,记卡片上的整式为A,再从剩下的卡片中任意抽取一张,记卡片上的整式为B,于是得到代数式 ![]() .
.
(1)请用画树状图或列表的方法,写出代数式 ![]() 所有可能的结果;
所有可能的结果;
(2)求代数式 ![]() 恰好是分式的概率.
恰好是分式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.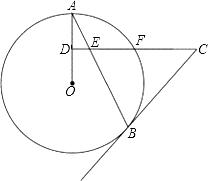
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果BE=10,sinA= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB内有一点P

(1)过点P画PC∥OB交OA于点C,画PD∥OA交OB于点D
(2)写出图中互补的角
(3)写出图中相等的角
(4)试说明图某一对相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )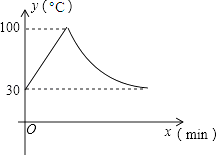
A.7:20
B.7:30
C.7:45
D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
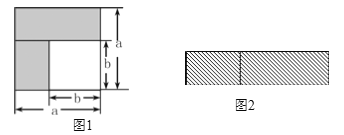
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p);②10.3×9.7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,△ABC的顶点坐标分别是A(-4,-1),B(1,1),C(-1,4);点![]() 是△ABC内一点,当点
是△ABC内一点,当点![]() 平移到点
平移到点![]() 时.
时.
①请写出平移后新![]() 三个顶点的坐标;
三个顶点的坐标;
②求![]() 的面积.
的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com