
【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.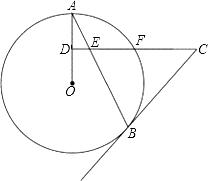
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果BE=10,sinA= ![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】
(1)证明:连接OB 
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC
又∵CD⊥OA
∴∠A+∠AED=∠A+∠CEB=90°
∴∠OBA+∠ABC=90°
∴OB⊥BC
∴BC是⊙O的切线
(2)解:连接OF,AF,BF, 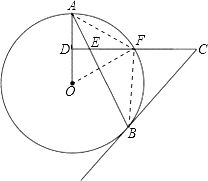
∵DA=DO,CD⊥OA,
∴AF=OF,
∵OA=OF,
∴△OAF是等边三角形,
∴∠AOF=60°
∴∠ABF= ![]() ∠AOF=30°
∠AOF=30°
(3)解:连接OF,AF, 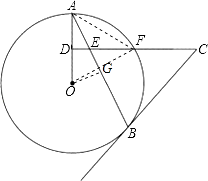
∵DA=DO,CD⊥OA,
∴AF=OF=OA,
过点O作OG⊥AB于点G,得到AG=BG,
在Rt△AOG中,sinA= ![]() =
= ![]() ,
,
设DE=5x,则AE=13x,AD=12x,AO=24x,
∵BE=10,∴AB=10+13x.
则AG= ![]() AB=5+
AB=5+ ![]() x,
x,
又∵直角△AOG中,sin∠BAO= ![]() ,则
,则 ![]() =
= ![]() ,
,
则 ![]() =
= ![]()
解得x= ![]() ,
,
∴AO=24x= ![]() .
.
【解析】(1)根据等边对等角,得到∠A=∠OBA,∠CEB=∠ABC,又CD⊥OA,由角的和差得到OB⊥BC,根据切线的判定方法得出BC是⊙O的切线;(2)根据垂直平分线定理,得到AF=OF,又OA=OF,得到△OAF是等边三角形,∠AOF=60°,所以∠ABF= ![]() ∠AOF=30°;(3)由DA=DO,CD⊥OA,得到AF=OF=OA,过点O作OG⊥AB于点G,得到AG=BG,在Rt△AOG中,sinA=
∠AOF=30°;(3)由DA=DO,CD⊥OA,得到AF=OF=OA,过点O作OG⊥AB于点G,得到AG=BG,在Rt△AOG中,sinA= ![]() ,由BE=10,得到AG=
,由BE=10,得到AG= ![]() AB,又直角△AOG中,sin∠BAO=
AB,又直角△AOG中,sin∠BAO= ![]() ,则
,则 ![]() =
= ![]()
![]() ,求出AO的值.
,求出AO的值.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】某学校跳绳活动月即将开始,其中有一项为跳绳比赛,体育组为了了解七年级学生的训练情况,随机抽取了七年级部分学生进行1分钟跳绳测试,并将这些学生的测试成绩(即1分钟的个数,且这些测试成绩都在60~180范围内)分段后给出相应等级,具体为:测试成绩在60~90范围内的记为![]() 级,90~120范围内的记为
级,90~120范围内的记为![]() 级,120~150范围内的记为
级,120~150范围内的记为![]() 级,150~180范围内的记为
级,150~180范围内的记为![]() 级.现将数据整理绘制成如下两幅不完整的统计图,其中在扇形统计图中
级.现将数据整理绘制成如下两幅不完整的统计图,其中在扇形统计图中![]() 级对应的圆心角为
级对应的圆心角为![]() ,请根据图中的信息解答下列问题:
,请根据图中的信息解答下列问题:
(1)在扇形统计图中,求![]() 级所占百分比;
级所占百分比;
(2)在这次测试中,求一共抽取学生的人数,并补全频数分布直方图;
(3)在(2)中的基础上,在扇形统计图中,求![]() 级对应的圆心角的度数.
级对应的圆心角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下叙述正确的有( )
①对顶角相等;②同位角相等;③两直角相等;④邻补角相等;⑤多边形的外角和都相等;⑥三角形的中线把原三角形分成面积相等的两个三角形
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥CD,E为AB、CD间的一点,连接EA、EC.
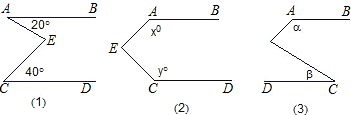
(1)如图①,若∠A=20°,∠C=40°,则∠AEC= °.
(2)如图②,若∠A=x°,∠C=y°,则∠AEC= °.
(3)如图③,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系.并简要说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=( )
A.60°
B.65°
C.72°
D.75°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com