
【题目】已知点A,B分别在反比例函数y= ![]() (x>0),y=
(x>0),y= ![]() (x>0)的图象上且OA⊥OB,则tanB为( )
(x>0)的图象上且OA⊥OB,则tanB为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:法一:
设点A的坐标为(x1, ![]() ),点B的坐标为(x2,﹣
),点B的坐标为(x2,﹣ ![]() ),
),
设线段OA所在的直线的解析式为:y=k1x,线段OB所在的直线的解析式为:y=k2x,
则k1= ![]() ,k2=﹣
,k2=﹣ ![]() ,
,
∵OA⊥OB,
∴k1k2= ![]() (﹣
(﹣ ![]() )=﹣1
)=﹣1
整理得:(x1x2)2=16,
∴tanB= ![]() =
=  =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
法二:过点A作AM⊥y轴于点M,过点B作BN⊥y轴于点N, 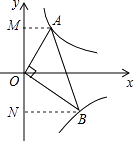
∴∠AMO=∠BNO=90°,
∴∠AOM+∠PAM=90°,
∵OA⊥OB,
∴∠AOM+∠BON=90°,
∴∠AOM=∠BON,
∴△AOM∽△OBN,
∵点A,B分别在反比例函数y= ![]() (x>0),y=
(x>0),y= ![]() (x>0)的图象上,
(x>0)的图象上,
∴S△AOM:S△BON=1:4,
∴AO:BO=1:2,
∴tanB= ![]() .
.
所以答案是:B.
【考点精析】关于本题考查的相似三角形的判定与性质和特殊角的三角函数值,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图所示是某班学生体重的频数分布直方图,则该班学生体重在40~45千克这一组的有________人,体重不足40千克的有________人.(注:40~45千克包括40千克,不包括45千克,其他同)
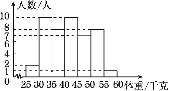
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 是直线
是直线![]() 上一点,且MN//PQ.
上一点,且MN//PQ.![]() 和
和![]() 的平分线交于点
的平分线交于点![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作直线交
作直线交![]() 于点
于点![]() (不与点
(不与点![]() 重合),交
重合),交![]() 于点E,
于点E,
①若点![]() 在点
在点![]() 的右侧,如图2,求证:
的右侧,如图2,求证:![]() ;
;
②若点![]() 在点
在点![]() 的左侧,则线段
的左侧,则线段![]() 、
、![]() 、
、![]() 有何数量关系?直接写出结论,不说理由.
有何数量关系?直接写出结论,不说理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )

A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点M、N分别表示数m,n. 则点M,N 之间的距离为|m-n|.已知点A,B,C,D在数轴上分别表示的数为a,b,c,d.且|a-c|=|b-c|=![]() |d-a|=1 (a≠b),则线段BD的长度为( )
|d-a|=1 (a≠b),则线段BD的长度为( )
A.3.5B.0.5C.3.5或0.5D.4.5或0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张卡片(形状、大小、颜色、质地都相等),正面分别写上整式x2+1,﹣x2﹣2,3.将这三张卡片背面向上洗匀,从中任意抽取一张卡片,记卡片上的整式为A,再从剩下的卡片中任意抽取一张,记卡片上的整式为B,于是得到代数式 ![]() .
.
(1)请用画树状图或列表的方法,写出代数式 ![]() 所有可能的结果;
所有可能的结果;
(2)求代数式 ![]() 恰好是分式的概率.
恰好是分式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.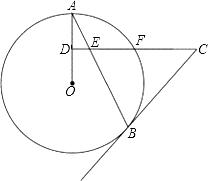
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果BE=10,sinA= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
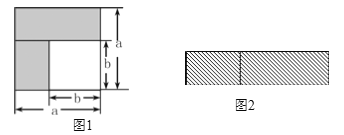
【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p);②10.3×9.7.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com