
����Ŀ��Ϊ�ƽ���ԭ���������裬�ٽ��в�����������ʡ������ͷ��ҵ֣���ղ�ʵ�м������£��ڱ�֤ԭ�������ߵ�ͬʱ�������µ������ߣ�����ij�¹�˾�ӵ�װ������2400���Ķ���������Ϊÿ��6��Ԫ����ֻ�����µ�����������������ԭ��������ȿ�����ǰ8����ɶ���������֪�µ�������ʹ����װ��Ч�ʱ���ǰ�����![]() ��
��
��1����ԭ������ÿ�����װ�������������
��2����֪ԭ������װ��һ��������Ҫ�ɱ�5��Ԫ���������߱�ԭ������ÿ����ʡ1��Ԫ�����ǹ�˾��������������ͬʱ����������������װ������������ԭ������װ��������2�����ʣ���η������������߲���ʹ��õ���������������Ϊ������Ԫ��
���𰸡���1��ԭ������ÿ�����װ��120��������2����ԭ����������800��������������������1600������ʱ����������������Ϊ4000��Ԫ
��������
��1�������������ԭ�����ߵĹ���Ч�ʣ����ù���ʱ�佨��������⼴�ɣ�
��2���������������ԭ�����ߵĹ����������ҳ��������ߵĹ�����������������֮��Ĺ�ϵ�����ҳ�δ֪���ķ�Χ����������ʾ��һ�κ���������һ�κ��������������������ֵ.
��1����ԭ������ÿ�����װ��![]() ����������
����������
![]() ����ã�
����ã�![]()
�����飬![]() ��ԭ��ʽ���̵ĸ�
��ԭ��ʽ���̵ĸ�
��ԭ������ÿ�����װ��120��������
��2����ԭ������װ��![]() ������������������װ�䣨2400��
������������������װ�䣨2400��![]() ����������
����������
2400��![]() ��2
��2![]()
��ã�![]() ��800��
��800��
��������ΪW��Ԫ����W����6��5��![]() +��6��4����2400��
+��6��4����2400��![]() ������
������![]() +4800��
+4800��
��Ϊ��1��0������W��![]() ���������С��
�����������
��![]() ��800
��800
���Ե�![]() ��800ʱ��W�������800+4800��4000����Ԫ����
��800ʱ��W�������800+4800��4000����Ԫ����
�𣺵�ԭ����������800��������������������1600������ʱ����������������Ϊ4000��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
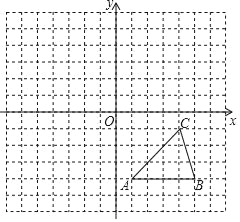
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC�������������ֱ�Ϊ��A��1����4����B��5����4����C��4����1����
��1������ABC����ƽ�Ƶõ���A1B1C1������C��Ӧ��C1������Ϊ��2��5����д����A��B�Ķ�Ӧ��A1��B1�����ꣻ
��2������ͼ������ϵ�л�����A1B1C1������������A1B1C1����ԭ��O�����ĶԳƵ���A2B2C2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=��k��2��x��3k2+12��
��1��kΪ��ֵʱ��ͼ��ԭ�㣻
��2��kΪ��ֵʱ��ͼ����ֱ��y=��2x+9�Ľ�����y���ϣ�
��3��kΪ��ֵʱ��ͼ��ƽ����y=��2x��ͼ��
��4��kΪ��ֵʱ��y��x�������С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���A=60�㣬BD��CD�ֱ�ƽ����ABC����ACB��M��N��Q�ֱ���DB��DC��BC���ӳ����ϣ�BE��CE�ֱ�ƽ����MBC����BCN��BF��CF�ֱ�ƽ����EBC����ECQ������F=________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�߲��������������½ϵ�ʱ����װ�к���ϵͳ�Ĵ�������һ������Ȼ�������¶�Ϊ18�������������������Ʒ�֣���ͼ��ij�����ϵͳ�ӿ������رռ��رպ������¶�y���棩��ʱ��x��Сʱ���仯�ĺ���ͼ������BC����˫����y=![]() ��һ���֣������ͼ����Ϣ����������⣺
��һ���֣������ͼ����Ϣ����������⣺
��1������ϵͳ�����챣�ִ������¶�18���ʱ���ж���Сʱ��
��2����k��ֵ��
��3����x=18ʱ�������ڵ��¶�ԼΪ���ٶȣ�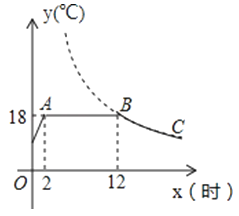
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������� ![]() �����н����У�����ȷ���ǣ� ��
�����н����У�����ȷ���ǣ� ��
A.ͼ��ؾ����㣨1��2��
B.y��x�����������
C.ͼ���ڵ�һ����������
D.��x��1����0��y��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ���ABC�ı߳�Ϊ2��CDΪAB���ϵ����ߣ�EΪ�߶�CD�ϵĶ��㣬��BEΪ�ߣ���BE������ȱ���BEF������DF����DF����СֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
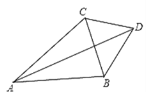
����Ŀ����ͼ,����ABC��,��BAC=40��,��ACB=60����DΪ��ABC��һ�㣬DAƽ�֡�BAC����CBD=50�������DCB�Ķ�����_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з������Ӧ����
5�·ݣ��ס�������������ˮ����Ϊ200�֣������ļ���ˮ�߷��ں�������������Ӧ���Һ��٣���ȡ��ˮ��ʩ.6�·ݣ�������ˮ����5�·ݼ�����15%���ҹ�����ˮ����5�·ݼ�����10%����������6�·���ˮ����Ϊ174�֣�����������5�·ݵ���ˮ�����Ƕ���?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com