
【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S=__;
(2)若AB>DC,则此时四边形ABCD的面积S′__S(用“>”或“=”或“<”填空).

【答案】(1)15;(2)=.
【解析】试题分析:(1)∵AB=DC,AB∥DC,
∴四边形ABCD是平行四边形,
∴四边形ABCD的面积S=5×3=15,
(2)如图,连接EC,延长CD、BE交于点P,
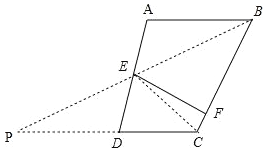
∵E是AD中点,
∴AE=DE,
又∵AB∥CD,
∴∠ABE=∠P,∠A=∠PDE,
在△ABE和△DPE中,
∵ ,
,
∴△ABE≌△DPE(AAS),
∴S△ABE=S△DPE,BE=PE,
∴S△BCE=S△PCE,
则S四边形ABCD=S△ABE+S△CDE+S△BCE
=S△PDE+S△CDE+S△BCE
=S△PCE+S△BCE
=2S△BCE
=2×![]() ×BC×EF
×BC×EF
=15,
∴当AB>DC,则此时四边形ABCD的面积S′=S,


科目:初中数学 来源: 题型:
【题目】(本小题满分9分)点A,B,C在数轴上表示数a,b,c,满足(b+2)2+(c–24)2=0,多项式x|a+3|y2–ax3y+xy2–1是关于字母x,y的五次多项式.
(1)a的值__________,b的值__________,c的值__________.
(2)已知蚂蚁从A点出发,以每秒3 cm的速度爬行,先到点B,再到点C,一共需要多长时间?(精确到秒)
(3)求值:a2b–bc.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上的一点,连接PA,PC.
(1)证明:∠PAB=∠PCB;
(2)在BC上截取一点E,连接PE,使得PE=PC,连接AE,判断△PAE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】满足下列条件的三角形中,是直角三角形的是( )
A.三角形的三边长满足关系a+b=c
B.三角形的三边长之比2:3:4
C.三角形的三边长分别为5、12、13
D.三角形的一边长等于另一边长的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
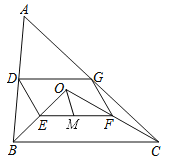
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用分式方程,解决下面问题:
为改善城市排水系统,某市需要新铺设一段全长为3 000m的排水管道。为了减少施工对城市交通的影响,实际施工时每天的工效是原计划的1.2倍,结果提前5天完成这一任务.
(1)这个工程队原计划每天铺设管道多少m?
(2)填空:在这项工程中,如果要求工程队提前6天完成任务,那么实际施工时每天的工效比原计划增加__________(填百分数,不写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“对顶角相等”,这个命题改写成“如果……那么……”的形式应该为________________________________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com