
 如图.在平面直角坐标系中,△OBC的顶点O与坐标原点重合,点B的坐标为(-6,2$\sqrt{7}$),OC=15,BC=17,求线段OB的长度和△OBC的面积.
如图.在平面直角坐标系中,△OBC的顶点O与坐标原点重合,点B的坐标为(-6,2$\sqrt{7}$),OC=15,BC=17,求线段OB的长度和△OBC的面积. 分析 在直角△OBM中利用勾股定理即可求得OB的长,然后根据勾股定理的逆定理证得△OBC是直角三角形,最后根据三角形面积公式即可求得三角形的面积.
解答 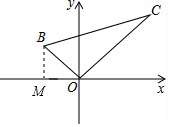 解:过点B作BM⊥x轴于点M,
解:过点B作BM⊥x轴于点M,
∵点B的坐标为(-6,2$\sqrt{7}$),
∴OM=6,BM=2$\sqrt{7}$,
由勾股定理得OB2=62+(2$\sqrt{7}$)2=64,
∴OB=8.
∵82+152=172,
∴OB2+OC2=BC2,
∴△OBC是直角三角形,且∠BOC=90°,
∴△OBC的面积=$\frac{1}{2}$×8×15=60.
点评 本题考查的是坐标和图形的性质,勾股定理和逆定理,熟知性质定理是解答此题的关键.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 章丘市积极推进新农村建设,在城区与每个乡镇之间都开通了每半小时一班的公 交车,如图,是通往某镇的甲、乙两辆公交车分别从客运中心和某镇两地出发相向而行的时间和距离客运中心的关系图,图中l1、l2表示两辆公交车与客运中心的距离S (千米)与行驶时间t(小时)之间的关系,则下列说法:
章丘市积极推进新农村建设,在城区与每个乡镇之间都开通了每半小时一班的公 交车,如图,是通往某镇的甲、乙两辆公交车分别从客运中心和某镇两地出发相向而行的时间和距离客运中心的关系图,图中l1、l2表示两辆公交车与客运中心的距离S (千米)与行驶时间t(小时)之间的关系,则下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com