
【题目】如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD等于( )
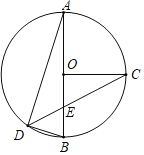
A.20°B.25°C.30°D.32.5°
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,直线![]() ,垂足为点
,垂足为点![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() .直线
.直线![]() 绕点
绕点![]() 按逆时针方向旋转,旋转角度为
按逆时针方向旋转,旋转角度为![]() .
.
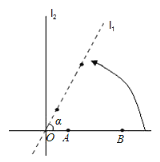
(1)当![]() 时,在直线
时,在直线![]() 上找点
上找点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰三角形,此时
为顶角的等腰三角形,此时![]() _____.
_____.
(2)当![]() 在什么范围内变化时,直线
在什么范围内变化时,直线![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰三角形,请用不等式表示
为顶角的等腰三角形,请用不等式表示![]() 的取值范围:_________.
的取值范围:_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
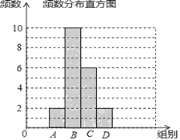
【题目】张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理,绘制了如下不完整的统计图表:
组别 | 步数分组 | 频率 |
A | x<6000 | 0.1 |
B | 6000≤x<7000 | 0.5 |
C | 7000≤x<8000 | m |
D | x≥8000 | n |
合计 | 1 |
根据信息解答下列问题:
(1)填空:m= ,n= ;并补全条形统计图;
(2)这20名朋友一天行走步数的中位数落在 组;(填组别)
(3)张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞,请求出甲、乙被同时点赞的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
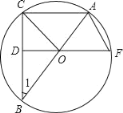
【题目】如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF.
(1)求证:△COD≌△BOD;
(2)填空:①当∠1= 时,四边形OCAF是菱形;
②当∠1= 时,AB=2![]() OD.
OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:
(1)AD=BD;
(2)DF是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(4,0),C(0,2)三点.
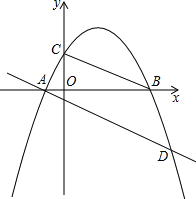
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E,使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
(3)若将直线BC平移,使其经过点A,且与抛物线相交于点D,连接BD,试求出∠BDA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
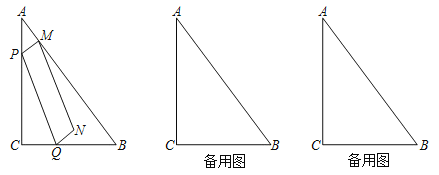
【题目】如图,已知在Rt△ABC中,∠C=90°,AC=8,BC=6,点P、Q分别在边AC、射线CB上,且AP=CQ,过点P作PM⊥AB,垂足为点M,联结PQ,以PM、PQ为邻边作平行四边形PQNM,设AP=x,平行四边形PQNM的面积为y.
(1)当平行四边形PQNM为矩形时,求∠PQM的正切值;
(2)当点N在△ABC内,求y关于x的函数解析式,并写出它的定义域;
(3)当过点P且平行于BC的直线经过平行四边形PQNM一边的中点时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
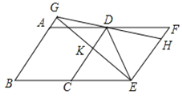
【题目】如图,把菱形![]() 向右平移至
向右平移至![]() 的位置,作
的位置,作![]() ,垂足为
,垂足为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() :④
:④![]() .
.
则其中所有成立的结论是( )
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com