
【题目】如图,在⊙O中,点C在优弧AB上,将弧BC沿BC折叠后刚好经过AB的中点D. 若⊙O的半径为![]() ,AB=8,则BC的长是( )
,AB=8,则BC的长是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
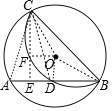
连接OD、AC、DC、OB、OC,作CE⊥AB于E,OF⊥CE于F,如图,利用垂径定理得到OD⊥AB,则AD=BD=![]() AB=4,于是根据勾股定理可计算出OD=2,再利用折叠的性质可判断弧AC和弧CD所在的圆为等圆,则根据圆周角定理得到
AB=4,于是根据勾股定理可计算出OD=2,再利用折叠的性质可判断弧AC和弧CD所在的圆为等圆,则根据圆周角定理得到![]() ,所以AC=DC,利用等腰三角形的性质得AE=DE=2,接着证明四边形ODEF为正方形得到OF=EF=2,然后计算出CF后得到CE=BE=6,由勾股定理可得到BC的长.
,所以AC=DC,利用等腰三角形的性质得AE=DE=2,接着证明四边形ODEF为正方形得到OF=EF=2,然后计算出CF后得到CE=BE=6,由勾股定理可得到BC的长.
连接OD、AC、DC、OB、OC,作CE⊥AB于E,OF⊥CE于F,如图.
∵D为AB的中点,∴OD⊥AB,∴AD=BD=![]() AB=4.
AB=4.
在Rt△OBD中,OD=![]() =2.
=2.
∵将弧![]() 沿BC折叠后刚好经过AB的中点D,∴弧AC和弧CD所在的圆为等圆,∴
沿BC折叠后刚好经过AB的中点D,∴弧AC和弧CD所在的圆为等圆,∴![]() ,∴AC=DC,∴AE=DE=2.
,∴AC=DC,∴AE=DE=2.
易证四边形ODEF为正方形,∴OF=EF=2.
在Rt△OCF中,CF=![]() =4,∴CE=CF+EF=4+2=6.
=4,∴CE=CF+EF=4+2=6.
而BE=BD+DE=4+2=6,∴BC=![]() .
.
故选C.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
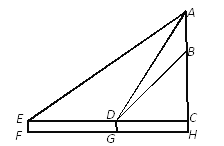
【题目】某学生为测量一棵大树AH及其树叶部分AB的高度,将测角仪放在F处测得大树顶端A的仰角为30°,放在G处测得大树顶端A的仰角为60°,树叶部分下端B的仰角为45°,已知点F、G与大树底部H共线,点F、G相距15米,测角仪高度为1.5米.求该树的高度AH和树叶部分的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
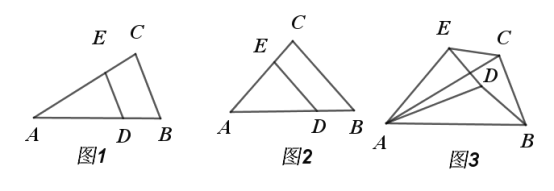
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上的动点,
边上的动点,![]() 交
交![]() 于点
于点![]() .
.
问题发现:(1)如图2,当![]() 时,
时,![]() ;
;![]() 与
与![]() 所在直线相交所成的锐角等于__________.
所在直线相交所成的锐角等于__________.
类比探究:(2)当![]() 时,把
时,把![]() 绕点
绕点![]() 逆时针旋转到如图3的位置时,请求出
逆时针旋转到如图3的位置时,请求出![]() 的值以及
的值以及![]() 与
与![]() 所在直线相交所成的锐角.
所在直线相交所成的锐角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD等于( )
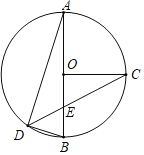
A.20°B.25°C.30°D.32.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节过后元宵节,欢聚一堂诉团圆,元宵节是我国传统节日,在这天家家都要吃元宵.妈妈买了4包元宵,每包一斤(4包元宵除馅不同外,外包装以及其它都相同),其中有两包黑芝麻馅的元宵、一包五仁馅的元宵、一包花生馅的元宵,妈妈从中任意拿出两包送给奶奶.
(1)妈妈随机拿出一包,求拿到黑芝麻馅元宵的概率是 ;
(2)用树状图或列表的方法求奶奶拿到的至少有一包黑芝麻馅元宵的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生全部参加“禁毒知识竞赛”,从中抽取了部分学生,将他们的竞赛成绩进行统计后分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等次,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题:
四个等次,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题:
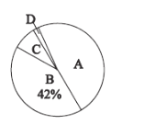
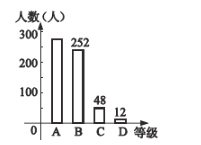
(1)抽取了_______名学生成绩;
(2)扇形统计图中![]() 等级所在扇形的圆心角度数是_________;
等级所在扇形的圆心角度数是_________;
(3)为估算全校八年级“禁毒知识竞赛”平均分,现将![]() 、
、![]() 、
、![]() 、
、![]() 依次记作
依次记作![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分,请估算该校八年级知识竞赛平均分.
分,请估算该校八年级知识竞赛平均分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD//BC,E是BC的中点,AD="5" cm,BC="12" cm,CD=![]() cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts.
cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts.
(1)当t为何值时以点P、A、D、E为顶点的四边形为直角梯形;
(2)当t为何值时以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?如能,请求出t值,如不能请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
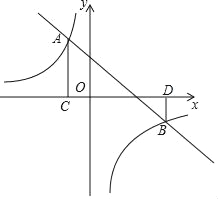
【题目】如图,直线y=﹣x+2与反比例函数y=![]() (k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(1)求a,b的值及反比例函数的解析式;
(2)若点P在直线y=﹣x+2上,且S△ACP=S△BDP,请求出此时点P的坐标;
(3)在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,请直接写出M点的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com