
【题目】如图,在梯形ABCD中,AD//BC,E是BC的中点,AD="5" cm,BC="12" cm,CD=![]() cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts.
cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts.
(1)当t为何值时以点P、A、D、E为顶点的四边形为直角梯形;
(2)当t为何值时以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?如能,请求出t值,如不能请说明理由.

【答案】(1)t=3s,t=8s;(2)t=1s,t=11s;(3)能,t=11s.
【解析】
(1)分AP⊥BC与DP⊥BC两种情况,求出BP的长度,然后根据时间=路程÷速度进行计算求解;
(2)根据平行四边形对边平行且相等,分点P在点E的左边与右边两种情况,PE=AD=5,然后求出BP的长度,再根据路程、时间、速度的关系求解;
(3)根据菱形是平行四边形,对(2)中的两种情况求出DE与PD的长度,如果等于AD的长度5,则是菱形,否则不是.
解:(1)如图1,过点A作AM⊥BC,DN⊥BC,垂足分别为M、N,当点P运动到M、N时为直角梯形,
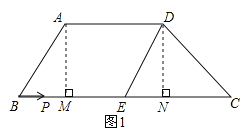
∵CD=![]() cm,∠C=45°,
cm,∠C=45°,
∴NC=4cm,
∵AD=5cm,
∴MN=AD=5cm,
①点P运动到M处时,AP⊥BC,BP=BM=BC-NC-MN=12-4-5=3cm,
∵点P的运动速度是1cm/s,
∴t=3÷1=3s;
②当点P运动到点N处时,DP⊥BC,
BP=BC-CN=12-4=8,
∴t=8÷1=8s;
(2)如图2,①当点P在点E的左边,AD=PE时,四边形APED是平行四边形,
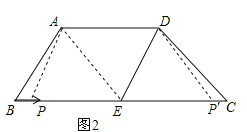
∵E是BC的中点,BC=12cm,
∴BE=![]() BC=6cm,
BC=6cm,
∵AD=5cm,
∴BP=BE-PE=6-5=1cm,
∴t=1÷1=1s;
②当点P在点E的右边,PE=AD时,四边形AEPD是平行四边形,
∵E是BC的中点,BC=12cm,
∴EC=![]() BC=6cm,
BC=6cm,
∵AD=5cm,
∴PC=EC-PE=6-5=1cm,
∴BP=BC-PC=12-1=11cm,
∴t=11÷1=11s;
(3)能是菱形.
如图3,过点D作DN⊥BC,垂足为N,若为菱形,必须是平行四边形,所以在(2)中两种情形中,
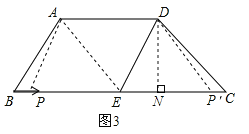
四边形APED是平行四边形时,
∵CD=![]() cm,∠C=45°,
cm,∠C=45°,
∴DN=4,EN=EC-CN=6-4=2,
∴DE=![]() cm,
cm,
∵AD=5cm,
∴AD≠DE,
∴平行四边形APED不是菱形;
②四边形AEPD是平行四边形时,
DN=4cm,PC=1cm,
∴PN=NC-PC=4-1=3cm,
∴DP=![]() cm,
cm,
∵AD=DP=5cm,
∴平行四边形AEPD是菱形;
综上所述,当t=11s时是菱形.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
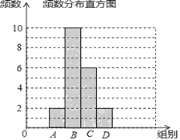
【题目】张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理,绘制了如下不完整的统计图表:
组别 | 步数分组 | 频率 |
A | x<6000 | 0.1 |
B | 6000≤x<7000 | 0.5 |
C | 7000≤x<8000 | m |
D | x≥8000 | n |
合计 | 1 |
根据信息解答下列问题:
(1)填空:m= ,n= ;并补全条形统计图;
(2)这20名朋友一天行走步数的中位数落在 组;(填组别)
(3)张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞,请求出甲、乙被同时点赞的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
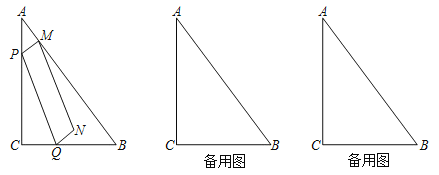
【题目】如图,已知在Rt△ABC中,∠C=90°,AC=8,BC=6,点P、Q分别在边AC、射线CB上,且AP=CQ,过点P作PM⊥AB,垂足为点M,联结PQ,以PM、PQ为邻边作平行四边形PQNM,设AP=x,平行四边形PQNM的面积为y.
(1)当平行四边形PQNM为矩形时,求∠PQM的正切值;
(2)当点N在△ABC内,求y关于x的函数解析式,并写出它的定义域;
(3)当过点P且平行于BC的直线经过平行四边形PQNM一边的中点时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=6![]() ,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为
,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为![]() ,并且CD⊥AC,则BC的长为________.
,并且CD⊥AC,则BC的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(![]() ,
,![]() m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )
A. x>![]() B.
B. ![]() <x<
<x<![]() C. x<
C. x<![]() D. 0<x<
D. 0<x<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把菱形![]() 向右平移至
向右平移至![]() 的位置,作
的位置,作![]() ,垂足为
,垂足为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() :④
:④![]() .
.
则其中所有成立的结论是( )
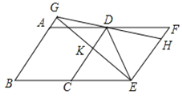
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》内容主要讲数学的用途,浅显易懂,其中有许多有趣的数学题,如“河边洗碗”.原文:今有妇人河上荡桮.津吏问曰:“桮何以多?“妇人曰:“家有客.”津吏曰:“客几何?”妇人日:“二人共饭,三人共羹,四人共肉,凡用桮六十五.不知客几何?“译文:有一名妇女在河边洗刷一大摞碗.一个津吏问她:“怎么刷这么多碗呢?“她回答:“家里来客人了.“津吏又问:“家里来了多少客人?”妇女答道:“2个人给一碗饭,3个人给一碗汤,4个人给一碗肉,一共要用65只碗,来了多少客人?”答:共有_____人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com