练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知关于x的一元二次方程

    (a＋c)x2＋2bx＋(a－c)＝0，其中a，b，c分别为△ABC三边的长．

    (1)如果x＝－1是方程的根，试判断△ABC的形状，并说明理由；

    (2)如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由．

    　


     (1)根据题意有a＋c－2b＋a－c＝0，即a＝b，∴△ABC为等腰三角形　(2)根据题意有Δ＝(2b)2－4(a＋c)(a－c)＝4b2－4a2＋4c2＝0，∴b2＋c2＝a2，∴△ABC为直角三角形　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    正比例函数与反比例函数的图象交于A、B两点，若

       点A的坐标是（1，2），则点B的坐标是___________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图,直升飞机在资江大桥AB的上方P点处，此时飞机离地面的高度PO=450米，且A、B、O三点在一条直线上，测得大桥两端的俯角分别为α=30°，β=45°，求大桥的长AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在三角形ABC中，∠B=350,AD是BC边上的高,且AD2=BD.CD,则∠BAC=       .  

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知tanA =，求sinA，cosA.                                 

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若△ABC∽△A′B′C′，相似比为1：2，则△ABC与△A′B′C′的面积的比为

    A．1：2                B．                      2：1                                  C．1：4       D．4：1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    4的平方根是         .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


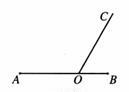
    如图1，点O在线段AB上，AO=2，OB=1，OC为射线，且∠BOC=60°，动点P以每秒2个单位长度的速度从点O出发，沿射线OC做匀速运动，设运动时间为t秒.

    （1）当t=秒时，则OP=      ，S△ABP=            ；

    （2）当△ABP是直角三角形时，求t的值；

    （3）如图2，当AP=AB时，过点A作AQ∥BP，并使得∠QOP=∠B，求证：AQ·BP=3.为了证明AQ·BP=3，小华同学尝试过O点作OE∥AP交BP于点E.试利用小华同学给我们的启发补全图形并证明AQ·BP=3．

    28题图2
     

    28题备用图
     

    28题图1
     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    a是2b的倒数，（﹣）5=　　　　　　．

    查看答案和解析>>

    同步练习册答案