
【题目】搬进新居后,小杰自己动手用彩塑纸做了一个如图所示的正方形的挂式小饰品ABCD,彩线BD.AN.CM将正方形ABCD分成六部分,其中M是AB的中点,N是BC的中点,AN与CM交于O点.已知正方形ABCD的面积为576cm2 , 则被分隔开的△CON的面积为( ) 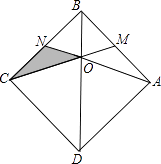
A.96cm2
B.48cm2
C.24cm2
D.以上都不对
【答案】B
【解析】
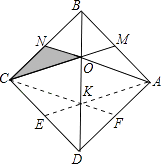
解答:解:找到CD的中点E,找到AD的中点F,连接CF,AE,
则CM∥EA,AN∥FC,△BOM∽△BKA,
∴ ![]() =
= ![]() =
= ![]() ,
,
同理可证: ![]() =
= ![]() =
= ![]() ,
,
故DK=KO=OB,
∴△BOC和△BOA的面积和为 ![]() 正方形ABCD的面积,
正方形ABCD的面积,
∵CN=NB=AM=BM,
∴△OCN的面积为 ![]() △BOC和△BOA的面积和,
△BOC和△BOA的面积和,
∴△OCN的面积为 ![]() =48cm2,
=48cm2,
故选B
分析:先证明BO为正方形ABCD的对角线BD的 ![]() ,再求证△CNO,△NBO,△AMO,△BMO的面积相等,即△CON的面积为正方形面积的
,再求证△CNO,△NBO,△AMO,△BMO的面积相等,即△CON的面积为正方形面积的 ![]() .本题考查了正方形内中位线的应用,考查了正方形四边均相等的性质,解本题的关键是求证BO=
.本题考查了正方形内中位线的应用,考查了正方形四边均相等的性质,解本题的关键是求证BO= ![]() BD,△OCN的面积为
BD,△OCN的面积为 ![]() △BOC和△BOA的面积和
△BOC和△BOA的面积和


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,根据图象回答下列问题:
(1)a 0;
(2)b 0;
(3)b2﹣4ac 0;
(4)y<0时,x的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线![]() (
(![]() )交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是y轴上的一个动点,请进行如下探究:
探究一:如图1,设△PAD的面积为S,令W=t·S,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.
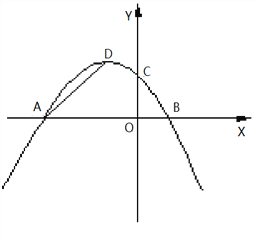
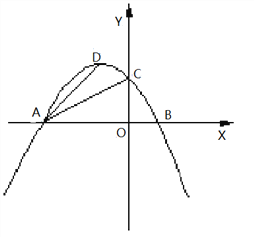
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( ) 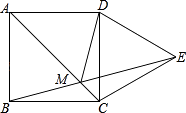
A.75°
B.60°
C.54°
D.67.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
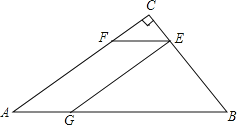
【题目】一块三角形废料如图所示,∠A=30°,∠C=90°,BC=6.用这块废料剪出一个平行四边形AGEF,其中,点G,E,F分别在AB,BC,AC上.设CE=x
(1)求x=2时,平行四边形AGEF的面积.
(2)当x为何值时,平行四边形AGEF的面积最大?最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com