
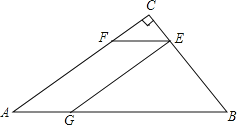
【题目】一块三角形废料如图所示,∠A=30°,∠C=90°,BC=6.用这块废料剪出一个平行四边形AGEF,其中,点G,E,F分别在AB,BC,AC上.设CE=x
(1)求x=2时,平行四边形AGEF的面积.
(2)当x为何值时,平行四边形AGEF的面积最大?最大面积是多少?
【答案】9![]() (平方单位)
(平方单位)
【解析】设平行四边形AGEF的面积是S.利用平行四边形AGEF的对边互相平行知EF∥AG,所以同位角∠A=∠CFE=30°;然后在直角三角形ABC和直角三角形BEF中利用锐角三角函数的定义求得CF、AC的长度,从而求得平行四边形AGEF的底边AF=AC-CF;最后根据平行四边形的面积公式S=底×高得出关于S与x的函数关系式S=-![]() x2+6
x2+6![]() x;
x;
(1)将x=2代入S与x的函数关系式S=-![]() x2+6
x2+6![]() x,并求解即可;
x,并求解即可;
(2)利用配方法求二次函数的最值.
解:设平行四边形AGEF的面积是S.
∵四边形AGEF是平行四边形,
∴EF∥AG;
∵∠A=30°,∠C=90°,CE=x,BC=6,
∴∠A=∠CFE=30°,
∴CF=![]() x,AC=6
x,AC=6![]() ,
,
∴AF=6![]() ﹣
﹣![]() x;
x;
∴S=AFCE=(6![]() ﹣
﹣![]() x)x=﹣
x)x=﹣![]() x2+6
x2+6![]() x,即S=﹣
x,即S=﹣![]() x2+6
x2+6![]() x;
x;
(1)当x=2时,S=﹣4![]() +12
+12![]() =8
=8![]() ,即S=8
,即S=8![]() .
.
答:平行四边形AGEF的面积为8![]() (平方单位)
(平方单位)
(2)由S=﹣![]() x2+6
x2+6![]() x,得S=-
x,得S=-![]() x2+6
x2+6![]() x,
x,
∴S=-![]() (x-3)2+9
(x-3)2+9![]() ,
,
∴当x=3时,平行四边形AGEF的面积最大,最大面积是9![]() (平方单位)
(平方单位)
“点睛”本题考查了平行四边形的性质、二次函数的最值.解答本题的关键是求出平行四边形AGEF的底边AF、底边上的高线CE的长度.


科目:初中数学 来源: 题型:
【题目】图①是一面矩形彩旗完全展平时的尺寸图(单位:cm).其中矩形ABCD是由双层白布缝制的穿旗杆用的旗裤,阴影部分DCEF为矩形绸缎旗面.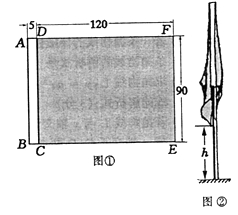
(1)用经加工的圆木杆穿入旗裤作旗杆,求旗杆的最大直径(精确到1cm);
(2)将穿好彩旗的旗杆垂直插在操场上,旗杆从旗顶到地面的高度为220cm.在无风的天气里,彩旗自然下垂,如图②.求彩旗下垂时最低处离地面的最小高度h.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.
(1)①当PC∥QB时,OQ= ;
②当PC⊥QB时,求OQ的长.
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】搬进新居后,小杰自己动手用彩塑纸做了一个如图所示的正方形的挂式小饰品ABCD,彩线BD.AN.CM将正方形ABCD分成六部分,其中M是AB的中点,N是BC的中点,AN与CM交于O点.已知正方形ABCD的面积为576cm2 , 则被分隔开的△CON的面积为( ) 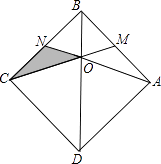
A.96cm2
B.48cm2
C.24cm2
D.以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①直线AB和直线BA是同一条直线;②平角是一条直线;③两点之间,线段最短;④如果AB=BC,则点B是线段AC的中点.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB交CD于E,交CB于F,且EG∥AB交CB于G,则CF与GB的大小关系是( )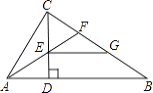
A.CF>GB
B.GB=CF
C.CF<GB
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30。 , 求∠ACF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com