
【题目】某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,现在采用提高售价,减少进货量的方法增加利润,已知这种商品每涨价0.5元,其销量就减少10件.
(1)要使每天获得利润700元,请你帮忙确定售价;
(2)问售价定在多少时能使每天获得的利润最多?并求出最大利润.
【答案】(1)13元或15元(2)14元,最大利润为720元
【解析】
解:(1)设每件商品提高x元,
则每件利润为(10+x-8)=(x+2)元,
每天销售量为(200-20x)件,
依题意,得:
(x+2)(200-20x)=700.
整理得:x2-8x+15=0.
解得:x1=3,x2=5.
∴把售价定为每件13元或15元能使每天利润达到700元;
答:把售价定为每件13元或15元能使每天利润达到700元.
(2)设应将售价定为x元时,才能使得所赚的利润最大为y元,
根据题意得:
y=(x-8)(200-![]() )
)
=-20x2+560x-3200,
=-20(x2-28x)-3200,
=-20(x2-28x+142)-3200+20×142
=-20(x-14)2+720,
∴x=14时,利润最大y=720.
答:应将售价提为14元时,才能使所赚利润最大,最大利润为720元.


科目:初中数学 来源: 题型:
【题目】文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
(1)甲乙两种图书的售价分别为每本多少元?
(2)书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD,
(1)求证:DF与⊙O的位置关系并证明;
(2)求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xoy中,点A、B的坐标分别是A(-1,0),B(3,0),将线段AB向上平移2个单位,再向右平移1个单位,得到线段DC,点A、B的对应点分别是D、C,连接AD、BC.
(1)直接写出点C,D的坐标;
(2)求四边形ABCD的面积;
(3)点P为线段BC上任意一点(与点B、C不重合),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2,图中各行从左到右列出的算筹数分别表示未知数![]() 的系数与相应的常数项,把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来就是
的系数与相应的常数项,把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来就是![]()
![]() 类似地,图2所示的算筹图我们可以用方程组形式表述为__________.
类似地,图2所示的算筹图我们可以用方程组形式表述为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为 1,CD⊥AB 于点 D,E 为射线 CD 上一点,以BE为边在 BE 左侧作等边△BEF,则DF的最小值为_____.
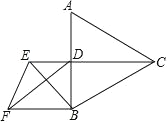
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),C(﹣1,2),且![]() .
.
(1)求a,b的值;
(2)y轴上是否存在一点M,使△COM的面积是△ABC的面积的一半,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 y=ax2+bx﹣![]() 与 x 轴交于 A(1,0)、B(6,0)两点,D 是 y 轴上一点,连接 DA,延长 DA 交抛物线于点 E.
与 x 轴交于 A(1,0)、B(6,0)两点,D 是 y 轴上一点,连接 DA,延长 DA 交抛物线于点 E.
(1)求此抛物线的解析式;
(2)若 E 点在第一象限,过点 E 作 EF⊥x 轴于点 F,△ADO 与△AEF 的面积比为![]() =
=![]() ,求出点 E 的坐标;
,求出点 E 的坐标;
(3)若 D 是 y 轴上的动点,过 D 点作与 x 轴平行的直线交抛物线于 M、N 两点, 是否存在点 D,使 DA2=DMDN?若存在,请求出点 D 的坐标;若不存在,请说 明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com