
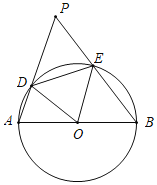
【题目】如图,⊙O中,AB为直径,点P为⊙O外一点,且PA=AB,PA、PB交⊙O于D、E两点,∠PAB为锐角,连接DE、OD、OE.
(1)求证:∠EDO=∠EBO;
(2)填空:若AB=8,
①△AOD的最大面积为 ;
②当DE= 时,四边形OBED为菱形.
【答案】(1)证明见解析;(2)8;4.
【解析】
(1)如图1,连AE,由等腰三角形的性质可知E为PB中点,则OE是△PAB的中位线,OE∥PA,可证得∠DOE=∠EOB,则∠EDO=∠EBO可证;
(2)如图2,由条件知OA=4,当OA边上的高最大时,△AOD的面积最大,可知点D是![]() 的中点时满足题意,此时最大面积为8;
的中点时满足题意,此时最大面积为8;
(3)如图3,当DE=4时,四边形ODEB是菱形.只要证明△ODE是等边三角形即可解决问题.
证明:(1)如图1,连AE,

∵AB为⊙O的直径,
∴∠AEB=90°,
∵PA=AB,
∴E为PB的中点,
∵AO=OB,
∴OE∥PA,
∴∠ADO=∠DOE,∠A=∠EOB
∵OD=OA,
∴∠A=∠ADO,
∴∠EOB=∠DOE,
∵OD=OE=OB,
∴∠EDO=∠EBO;
(2)①∵AB=8,
∴OA=4,
当OA边上的高最大时,△AOD的面积最大(如图2),此时点D是![]() 的中点,
的中点,
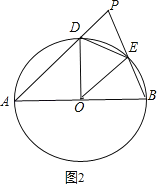
∴OD⊥AB,
∴![]() ;
;
②如图3,当DE=4时,四边形OBED为菱形,理由如下:
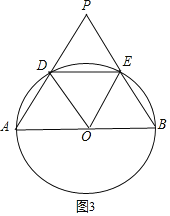
∵OD=DE=OE=4,
∴△ODE是等边三角形,
∴∠EDO=60°,
由(1)知∠EBO=∠EDO=60°,
∴OB=BE=OE,
∴四边形OBED为菱形,
故答案为:8;4.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】如图,在顶点为P的抛物线y=a(x-h)2+k(a≠0)的对称轴1的直线上取点A(h,k+![]() ),过A作BC⊥l交抛物线于B、C两点(B在C的左侧),点和点A关于点P对称,过A作直线m⊥l.又分别过点B,C作直线BE⊥m和CD⊥m,垂足为E,D.在这里,我们把点A叫此抛物线的焦点,BC叫此抛物线的直径,矩形BCDE叫此抛物线的焦点矩形.
),过A作BC⊥l交抛物线于B、C两点(B在C的左侧),点和点A关于点P对称,过A作直线m⊥l.又分别过点B,C作直线BE⊥m和CD⊥m,垂足为E,D.在这里,我们把点A叫此抛物线的焦点,BC叫此抛物线的直径,矩形BCDE叫此抛物线的焦点矩形.
(1)直接写出抛物线y=![]() x2的焦点坐标以及直径的长.
x2的焦点坐标以及直径的长.
(2)求抛物线y=![]() x2-
x2-![]() x+
x+![]() 的焦点坐标以及直径的长.
的焦点坐标以及直径的长.
(3)已知抛物线y=a(x-h)2+k(a≠0)的直径为![]() ,求a的值.
,求a的值.
(4)①已知抛物线y=a(x-h)2+k(a≠0)的焦点矩形的面积为2,求a的值.
②直接写出抛物线y=![]() x2-
x2-![]() x+
x+![]() 的焦点短形与抛物线y=x2-2mx+m2+1公共点个数分别是1个以及2个时m的值.
的焦点短形与抛物线y=x2-2mx+m2+1公共点个数分别是1个以及2个时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则![]() 的值是( )
的值是( )
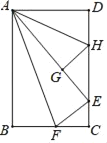
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】移动通信公司建设的钢架信号塔(如图1),它的一个侧面的示意图(如图2).CD是等腰三角形ABC底边上的高,分别过点A、点B作两腰的垂线段,垂足分别为B1,A1,再过A1,B1分别作两腰的垂线段所得的垂足为B2,A2,用同样的作法依次得到垂足B3,A3,….若AB为3米,sinα=![]() ,则水平钢条A2B2的长度为( )
,则水平钢条A2B2的长度为( )
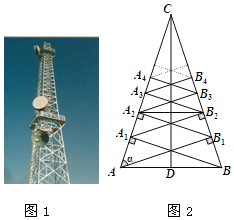
A. ![]() 米B. 2米C.
米B. 2米C. ![]() 米D.
米D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
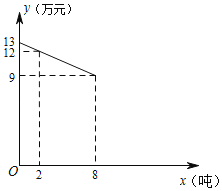
【题目】温州茶山杨梅名扬中国,某公司经营茶山杨梅业务,以3万元/吨的价格买入杨梅,包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(2≤x≤10,单位:吨)之间的函数关系如图所示.
(1)若杨梅的销售量为6吨时,它的平均销售价格是每吨多少万元?
(2)当销售数量为多少时,该经营这批杨梅所获得的毛利润(w)最大?最大毛利润为多少万元?(毛利润=销售总收入﹣进价总成本﹣包装总费用)
(3)经过市场调查发现,杨梅深加工后不包装直接销售,平均销售价格为12万元/吨.深加工费用y(单位:万元)与加工数量x(单位:吨)之间的函数关系是y=![]() x+3(2≤x≤10).
x+3(2≤x≤10).
①当该公司买入杨梅多少吨时,采用深加工方式与直接包装销售获得毛利润一样?
②该公司买入杨梅吨数在 范围时,采用深加工方式比直接包装销售获得毛利润大些?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(
的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5G网络是第五代移动通信网络,它将推动我国数字经济发展迈上新台阶. 据预测,2020年到2030年中国5G直接经济产出和间接经济产出的情况如下图所示.
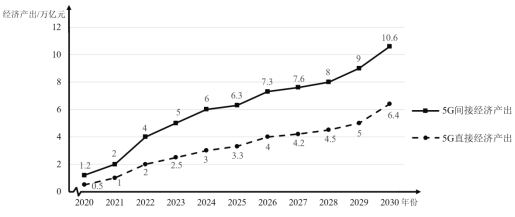
根据上图提供的信息,下列推断不合理的是( )
A.2030年5G间接经济产出比5G直接经济产出多4.2万亿元
B.2020年到2030年,5G直接经济产出和5G间接经济产出都是逐年增长
C.2030年5G直接经济产出约为2020年5G直接经济产出的13倍
D.2022年到2023年与2023年到2024年5G间接经济产出的增长率相同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系xOy 中,抛物线y=ax2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y轴交于点C
.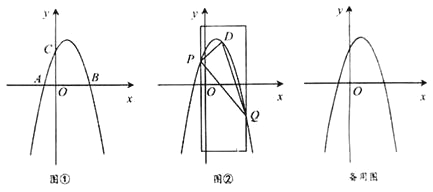
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、 Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP、DQ.
①若点P的横坐标为![]() ,求△DPQ面积的最大值,并求此时点D 的坐标;
,求△DPQ面积的最大值,并求此时点D 的坐标;
②直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com