
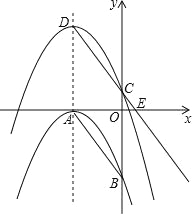
【题目】如图,抛物线C1:y=﹣![]() (x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E,
(x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E,
(1)求A,B点的坐标;
(2)当CE:CD=1:2时,求此时抛物线C2的顶点坐标;
(3)若四边形ABCD是菱形.
①此时抛物线C2的解析式;
②点F在抛物线C2的对称轴上,且点F在第三象限,点M在抛物线C2上,点P是坐标平面内一点,是否存在以A,F,P,M为顶点的四边形与菱形ABCD相似,并且这个菱形以A为顶点的角是钝角,若存在求出点F的坐标,若不存在请说明理由.
【答案】(1)A(﹣3,0),B(0,﹣4);(2)(3,2)(3,6)(3)①![]() ②
②![]() ,
,![]() ,
,![]()
【解析】
试题分析:(1)利用坐标轴上点的特点,确定出点A,B的坐标;
(2)根据锐角三角函数的意义,和抛物线的平移,得到比例式,求出即可;
(3)①由点的移动情况判断出抛物线的移动情况;
②设出点的坐标,M(3+3a,4a),表示出F(3,﹣5a).根据点在抛物线上,求出a,从而得到F的坐标.
试题解析:(1)令y=0,
∴y=﹣![]() (x+3)2=0,
(x+3)2=0,
∴x=3,
令x=0,
∴y=4,
∴A(﹣3,0),B(0,﹣4);
(2)由(1)得:OA=3,OB=4,
∴tan∠OBA=![]() .
.
由题意得AB∥CD,∠EDA=∠OBA,
∴![]() .
.
①当点C在y轴负半轴时,
由CE:CD=1:2,
∴OE=EA=1.5,AD=2,
∴D(3,2);
②当点C在y轴正半轴时,
由CE:CD=1:2,
∴OE:OA=1:2,
∴AE=4.5,
∴AD=6,
∴D(3,6).
(3)①由解析式可得A(﹣3,0),B(0,﹣4),
∴AB=BC=AD=DC=5,
即抛物线向上平移5个单位,因此抛物线C2
解析式为![]() ;
;
②I:如图,以AF为边在对称轴右侧作菱形时,延长BA,与抛物线C2 交于点G,
∴∠FAG=∠BAD.
当AF=AM时,点M与点G重合,菱形AMPF∽菱形ABCD,
∵tan∠AMP=tan∠OBA=![]()
∴设M(3+3a,4a),F(3,﹣5a).
把M点坐标代入![]() ,
,
可得a1=![]() ﹣1,
﹣1,![]() (舍去),
(舍去),
![]() .
.
当AF=AP时,
∴设M(3+3a,﹣a),F(3,﹣5a).
把M点坐标代入![]() ,
,
可得a1=﹣1 (舍去),![]() ,
,
![]() .
.
以AF为边在对称轴左侧作菱形时,点F坐标不变.
II:以AF为对角线作菱形时,
由菱形的对角线性质可知,
在AF右侧作∠FAP=∠FAM,
∴∠PAF=∠GAF=∠BAD,
菱形的轴对称性可得P点也在抛物线C2 上.
设M(3+3a,﹣a),F(3,﹣2a),
∴![]() ,
,
∴![]() .
.
当点M在AF左侧时,F点坐标不变.
当点M在AF左侧时,F点坐标不变.
综上所述:![]() ,
,![]() ,
,![]()


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】下列结论中,不正确的是( )
A. 两点确定一条直线
B. 两点之间,直线最短
C. 等角的余角相等
D. 过直线外一点,有且只有一条直线与已知直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )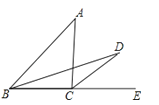
A.46°
B.92°
C.44°
D.23°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A.平行四边形的对角线一定相等
B.等腰三角形任意一条边上的高线、中线和角平分线都三线合一
C.三角形的中位线平行于第三边并且等于它的一半
D.三角形的两边之和小于第三边
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,小王想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行射击10次,它们的平均成绩均为7环,10次射击成绩的方差分别是:S2甲=3,S2乙=1.2.成绩较为稳定的是______.(填“甲”或“乙”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com