
【题目】已知一次函数y=kx+b的图象经过点(0,1),且与正比例函数y=![]() x的图象相交于点(2,a).
x的图象相交于点(2,a).

求:(1)a的值;
(2)一次函数y=kx+b的解析式;
(3)在图中画出这两个函数图象,并求这两个函数图象与x轴所围成的三角形面积.
【答案】(1)a=1;(2)![]() ;(3)画这两个函数图象见解析;面积为
;(3)画这两个函数图象见解析;面积为![]() .
.
【解析】
(1)将点(2,a)代入正比例函数y=![]() x中,即可求出a的值;
x中,即可求出a的值;
(2)将(0,1)和(2,1)分别代入一次函数y=kx+b中,即可求出一次函数的解析式;
(3)利用两点法画出两函数的图像,然后根据三角形的面积公式计算面积即可.
解:(1)将点(2,a)代入正比例函数y=![]() x中,得:a=
x中,得:a=![]() ×2=1;
×2=1;
(2)∵将(0,1)和(2,1)分别代入一次函数y=kx+b中,得
![]()
解得:![]()
∴一次函数的解析式为:![]() ;
;
(3)根据一次函数过点(0,1)和点(2,1),画出![]() 的图像;根据正比例函数过点(0,0)和点(2,1),画出y=
的图像;根据正比例函数过点(0,0)和点(2,1),画出y=![]() x的图像,如图所示,直线
x的图像,如图所示,直线![]() 和直线y=
和直线y=![]() x即为所求.
x即为所求.
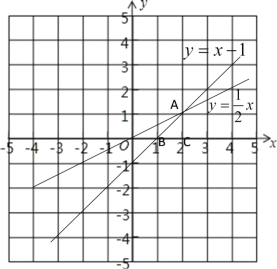
如上图所示,∵点A的坐标为(2,1)
∴AC=1
将y=0代入![]() 中,解得:
中,解得:![]()
∴B点坐标为(1,0)
∴OB=1
∴这两个函数图象与x轴所围成的三角形面积:S△AOB=![]() OB·AC=
OB·AC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H作直线l⊥AO于H,分别交直线AB、AC、BC、于点N、E、M.
(1)当直线l经过点C时(如图2),求证:BN=CD;
(2)当M是BC中点时,写出CE和CD之间的等量关系,并加以证明;
(3)请直接写出BN、CE、CD之间的等量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电商销售一款时装,进价![]() 元/件,售价
元/件,售价![]() 元/件,每天销售
元/件,每天销售![]() 件,每销售一件需缴纳平台推广费
件,每销售一件需缴纳平台推广费![]() 元.该电商计划开展降价促销活动,通过市场调研发现,该时装售价每降
元.该电商计划开展降价促销活动,通过市场调研发现,该时装售价每降![]() 元,每天销量增加
元,每天销量增加![]() 件.为保证市场稳定,供货商规定售价不得低于
件.为保证市场稳定,供货商规定售价不得低于![]() 元/件.问该电商对这款时装的每件售价定为多少元才能使每天扣除平台推广费之后的利润达到
元/件.问该电商对这款时装的每件售价定为多少元才能使每天扣除平台推广费之后的利润达到![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(2k+3)+k2+3k-4=0.
(1) 试判断上述方程根的情况并说明理由;
(2) 若以上一元二次方程的两个根分别为![]() 、
、![]() (
(![]() ),
),
① m=________,n=_________;
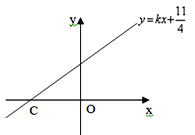
②当![]() 时,点A、B分别是直线
时,点A、B分别是直线![]() :y=kx+
:y=kx+![]() 上两点且A、B两点的横坐标分别为
上两点且A、B两点的横坐标分别为![]() 、
、![]() ,直线
,直线![]() 与
与![]() 轴相交于点C,若S△BOC=2S△AOC,求
轴相交于点C,若S△BOC=2S△AOC,求![]() 的值;
的值;
(3)在(2)的条件下,问在![]() 轴上是否存在点Q,使△ABQ的三个内角平分线交点在
轴上是否存在点Q,使△ABQ的三个内角平分线交点在![]() 轴上?若存在,求出点Q的坐标,若不存在,请说明理由.
轴上?若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交AC于点D,动点P在抛物线对称轴上,动点Q在抛物线上.
(1)求抛物线的解析式;
(2)当PO+PC的值最小时,求点P的坐标;
(3)是否存在以A,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD在直角坐标系中,边BC在x轴上,B点坐标为(m,0)且m>0.AB=a,BC=b,且满足b=![]() .
.
(1)求a,b的值及用m表示出点D的坐标;
(2)连接OA,AC,若△OAC为等腰三角形,求m的值;
(3)△OAC能为直角三角形吗?若能,求出m的值;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2018年高中一年级学生开始,湖南省全面启动高考综合改革,学生学习完必修课程后,可以根据高校相关专业的选课要求和自身兴趣、志向、优势,从思想政治、历史、地理、物理、化学、生物6个科目中,自主选择3个科目参加等级考试.学生![]() 已选物理,还想从思想政治、历史、地理3个文科科目中选1科,再从化学、生物2个理科科目中选1科.若他选思想政治、历史、地理的可能性相等,选化学、生物的可能性相等,则选修地理和生物的概率为___________.
已选物理,还想从思想政治、历史、地理3个文科科目中选1科,再从化学、生物2个理科科目中选1科.若他选思想政治、历史、地理的可能性相等,选化学、生物的可能性相等,则选修地理和生物的概率为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个整数能表示成a2+b2(a、b是正整数)的形式,则称这个数为“丰利数”.例如,2是“丰利数”,因为2=12+12,再如,M=x2+2xy+2y2=(x+y)2+y2(x+y,y是正整数),所以M也是“丰利数”.
(1)请你写一个最小的三位“丰利数”是 ,并判断20 “丰利数”.(填是或不是);
(2)已知S=x2+y2+2x﹣6y+k(x、y是整数,k是常数),要使S为“丰利数”,试求出符合条件的一个k值(10≤k<200),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下面的网格图中按要求画出图形,并回答问题:
(1)先画出△ABC向下平移5格后的△A1B1C1,再画出△ABC以点O为旋转中心,沿逆时针方向旋转90°后得到的△A2B2C2;
(2)如图,以点O为原点建立平面直角坐标系,试写出点A2,B1的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com