练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某电商销售一款时装，进价元/件，售价元/件，每天销售件，每销售一件需缴纳平台推广费元．该电商计划开展降价促销活动，通过市场调研发现，该时装售价每降元，每天销量增加件．为保证市场稳定，供货商规定售价不得低于元/件．问该电商对这款时装的每件售价定为多少元才能使每天扣除平台推广费之后的利润达到元？

    【答案】每件售价定为元才能使每天扣除平台推广费之后的利润达到元

    【解析】

    设降价x元后利润达到4500元.则每天可售出(20+4x)件,每件盈利(110-40-5-x)元.再根据相等关系:每天的获利=每天售出的件数×每件的盈利;列方程求解即可.

    设降价x元后利润达到4500元,
    由题意得: (110-40-5-x) (20+4x)=4500
    解得:,
    又∵售价不得低于80元/件,
    ∴取x=20,即售价为90元/件,
    答:每件售价定为90元才能使每天扣除平台推广费之后的利润达到4500元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC＝CD，

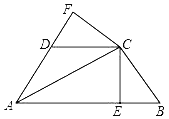
    （1）求证：△BCE≌△DCF；

    （2）若AB＝21，AD＝9，BC＝CD＝10，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知等腰Rt△ABC，∠ACB=90°，CA=CB，以BC为边向外作等边△CBA，连接AD，过点C作∠ACB的角平分线与AD交于点E，连接BE．

    （1）若AE=2，求CE的长度；

    （2）以AB为边向下作△AFB，∠AFB=60°，连接FE，求证：FA+FB= FE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

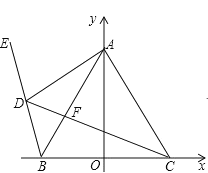
    【题目】如图，已知 B 1, 0 ， C 1, 0 ， A 为 y 轴正半轴上一点， AB AC ，点 D 为第二象限一动点，E 在 BD 的延长线上， CD 交 AB 于 F ，且BDC BAC .

    （1）求证： ABD ACD ；

    （2）求证： AD 平分CDE ；

    （3）若在 D 点运动的过程中，始终有 DC DA DB ，在此过程中，BAC 的度数是否变化？如果变化，请说明理由；如果不变，请求出BAC 的度数？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，CA=CB，CD=CE，∠ACB=∠DCE=α．

    （1）求证：BE=AD；

    （2）当α=90°时，取AD，BE的中点分别为点P、Q，连接CP，CQ，PQ，如图②，判断△CPQ的形状，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：

    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解下列方程.

    （1）2(1-x)2-8=0 （2 ）2x2x-1=0 （公式法）

    (3)x2-3x+1=0(配方法) (4) （x-1）2-5（x-1）+6=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=kx+b的图象经过点(0，1)，且与正比例函数y=x的图象相交于点(2，a).

    求：(1)a的值；

    (2)一次函数y=kx+b的解析式；

    (3)在图中画出这两个函数图象，并求这两个函数图象与x轴所围成的三角形面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请阅读下列材料：

    问题：如图，在正方形和平行四边形中，点，，在同一条直线上，是线段的中点，连接，．

    探究：当与的夹角为多少度时，平行四边形是正方形？

    小聪同学的思路是：首先可以说明四边形是矩形；然后延长交于点，构造全等三角形，经过推理可以探索出问题的答案．

    请你参考小聪同学的思路，探究并解决这个问题．

    （1）求证：四边形是矩形；

    （2）与的夹角为________度时，四边形是正方形．

    理由：

    查看答案和解析>>

    同步练习册答案