
����Ŀ������ڼ䣬С����Сӱ���ҹ�8����Լ������У��ֱ�����������ǰ�������ھ������11ǧ�״�һ�������˹��ϲ��ܼ�����ʻ.��ʱ�����ֹͣ�����ǻ���������30���ӣ�Ψһ�������õĽ�ͨ����ֻ����һ���������ͬ˾��������5�ˣ�����ÿСʱ60ǧ��.
(1)������������������ͣ�����4�˳˳����ߣ�����4��ԭ�صȺ�8���ܷ�ʱ������������ǻ�������(���³�ʱ����Բ���)
(2)������������͵�һ�����˵�ʱ�����µ�����ÿСʱ6ǧ���ٶȲ���ǰ����������˾������һ�������ʹ���������ؽӵڶ������ˣ������ܼ�ʱ���������
���𰸡�(1)8�˲��ܼ�ʱ������������Ǽ�������(2)���Dz��ܼ�ʱ�������.
��������
��1������·�̡��ٶȡ�ʱ��֮��ĵ�����ϵ��������𰸣�
��2�������µ��˹�������xСʱ��Ȼ�������������ĵ�����ϵ��������𰸣�
��1���������֪������������3��ȫ�̣�
��3��11=33ǧ�ף��������˵������������![]() Сʱ����33���ӣ���8�˲��ܼ�ʱ������������Ǽ�������
Сʱ����33���ӣ���8�˲��ܼ�ʱ������������Ǽ�������
��8�˲��ܼ�ʱ������������Ǽ�������
��2�������µ��˹�������xСʱ��
����������һ�ε�������ٷ��ؽ����µ���ʱ�������ˣ�60x��11��ǧ�ף���6x+60x��11=11��
��ã�x![]() ��
��
�����µ��˹�����22���ӣ���ӽӵ����µ��˺ڶ��ε��������ʱ��Ϊ��![]() Сʱ��8.8���ӣ�
Сʱ��8.8���ӣ�
���������˴ﵽ����������30.8���ӣ�Ҳ�Dz��ܼ�ʱ���������
�����͵�һ�����˵�ʱ�����µ�����ÿСʱ6ǧ���ٶȲ���ǰ����������˾������һ�������ʹ���������ؽӵڶ������ˣ����Dz��ܼ�ʱ���������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD�У�AB��CD��AB=8��DC=4����M��N�ֱ�Ϊ��AB��DC���е㣬��P�ӵ�D��������ÿ��1����λ���ٶȴ�D��C�����˶��������C��ֹͣ�˶���ͬʱ��Q�ӵ�B��������ÿ��3����λ���ٶȴ�B��A�����˶��������A������ԭ·���أ���P�����C���Qͬʱֹͣ�˶������P��Q�˶���ʱ��Ϊt�룬���Ե�M��N��P��QΪ������ı���Ϊƽ���ı���ʱ��t��ֵΪ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ȼ���������ǵ�������ɾ��Ļ�ʯ��Դ�����㷺���������������У�2019��1��1����ij��Ȼ������˾�Ծ�����������Ȼ�����е������±�Ϊ2018�ꡢ2019������Ľ��ݼ۸�
���� | �û��������� ����λ�������ף� | 2018�굥�� ����λ��Ԫ/�����ף� | 2019�굥�� ����λ��Ԫ/�����ף� |
��һ���� | 0-300������ |
| 3 |
�ڶ����� | 300-600������ |
| 3.5 |
�������� | 600���� |
| 5 |
��1�����û���2018����������Ϊ280�����ף����ܷ���Ϊ Ԫ���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2�����û���2018����������Ϊ450�����ף��ܷ���Ϊ1200Ԫ����![]() ��ֵ��
��ֵ��
��3���ڣ�2���������£����û���2018���2019�깲����Ȼ��1200�����ף�2018������������2019�����������ܷ���Ϊ3625Ԫ������û�2018���2019��ֱ��������������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ��������
����һ�����һ���������ĸ�λ���ֵ��ڳ���λ����֮���������λ����֮�ͣ���������Ϊ���������������磺��1+2=3������123��������������ͬ����55��1315Ҳ��������������
���϶�������![]() ����λ��������������������x��2��x��x+2�ֱ���������İ�λ���֣�ʮλ���֣���λ���֣����磺135��468��Ϊ����������
����λ��������������������x��2��x��x+2�ֱ���������İ�λ���֣�ʮλ���֣���λ���֣����磺135��468��Ϊ����������
���⣺
��1����֪a����������������������������������b��b��0��ʹ10a+bΪһ����������������b����Сֵ��
��2����֪һ����λ����������![]() ��һ�������������ĺ��ܱ�3��������c��a+d��b=4��֤��
��һ�������������ĺ��ܱ�3��������c��a+d��b=4��֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2018�����������λ�У�ij�����ƻ������Ϊ1600m2����������̻�����Ͷ�꣬�ɼס����������̶�����ɣ�����ÿ��������̻���������Ҷ�ÿ��������̻������2���������ڶ���������Ϊ400m2������̻�ʱ���ӱ��Ҷ�����5�죮
(1)��ס��������̶�ÿ��������̻��������
(2)����̶�ʩ��x�죬�ҹ��̶�ʩ��y�죬�պ�����̻�������y����x�ĺ�����ϵʽ��
(3)����ÿ���̻�������0.6��Ԫ���Ҷ�ÿ���̻�����Ϊ0.25��Ԫ���Ҽ�������ʩ����������������25�죬����ΰ��ż�������ʩ����������ʹʩ���ܷ�����ͣ��������ͷ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
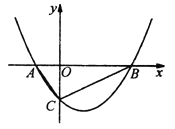
����Ŀ����ͼ��������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ���䶥����ֱ��
���䶥����ֱ��![]() ��.
��.
��1����![]() ��ֵ;
��ֵ;
��2����![]() ���������;
���������;
��3����![]() Ϊһ���ڱ���
Ϊһ���ڱ���![]() �����
�����![]() ����
����![]() ��ĶԳƵ�
��ĶԳƵ�![]() �Ƿ��ڸ���������?
�Ƿ��ڸ���������?
��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪���⡿
��ͼ�٣���C���߶�AB�ϣ�ͼ�й��������߶�AB��AC��BC����������һ���߶εij���������һ���߶γ��ȵ�2������Ƶ�C���߶�AB�����ɵ���.
�߶ε��е�__________�����߶ε����ɵ���������������������������.
��AB = 12cm����C���߶�AB���ɵ㣬��AC=___________cm��
��������⡿
��3�� ��ͼ�ڣ���֪AB=12cm.����P�ӵ�A��������2cm/s���ٶ���AB���B�����ƶ�����Q�ӵ�B��������1cm/s���ٶ���BA���A�����ƶ�����P��Qͬʱ������������һ�㵽���յ�ʱ���˶�ֹͣ�����ƶ���ʱ��Ϊt��s��.��tΪ��ֵʱ��A��P��Q����������һ��ǡ������������Ϊ�˵���߶ε��ɵ㣿˵������

![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ӳ���ѵ������Ҫ��Ŀ֮һ������ͼ���е������Ǽס��ҡ�������ÿ��ʮ�ε�����Եijɼ������Թ���Ϊ��������10����ÿ����λ1����1�֣�
���������������������˶�Ա�ײ��Գɼ���
������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�ɼ����֣� | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |


��1��д���˶�Ա�ײ��Գɼ�������Ϊ_____���˶�Ա�Ҳ��Գɼ�����λ��Ϊ_____���˶�Ա�����Գɼ���ƽ����Ϊ_____��
��2�����������˳ɼ��ķ���ֱ�ΪS��2=0.8��S��2=0.4��S��2=0.8�����ۺϷ�����������������ѡ��һλ����ɼ������ҽ�Ϊ�ȶ��Ľ���������Ϊ�����ˣ�����Ϊѡ˭�����ʣ�Ϊʲô��
��3���ס��ҡ��������֮����е�����ϰ��ÿ���˵��ȿ��ܵĴ����������ˣ������ȴӼ����д����������ֽ���ʱ��ص������еĸ����Ƕ��٣�������״ͼ���б������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о���ʹ������ˮ�����±��շ�(ˮ�Ѱ��½���)
������ˮ�� | ���� |
������ | 2Ԫ/ |
���� | 3Ԫ/ |
���� | 4Ԫ/ |
(1)ij�û�һ��������![]() ˮ������û����ɵ�ˮ����______Ԫ��
ˮ������û����ɵ�ˮ����______Ԫ��
(2)ij������ˮ��Ϊ![]() ������(10<x��20)�����û����ɵ�ˮ����______Ԫ(�ú�
������(10<x��20)�����û����ɵ�ˮ����______Ԫ(�ú�![]() ����ʽ��ʾ)
����ʽ��ʾ)
(3)һ�·ݼס������û�����ˮ![]() ������û���ˮ��Ϊ
������û���ˮ��Ϊ![]() ����
����![]() ������������¹���ˮ��105Ԫ����
������������¹���ˮ��105Ԫ����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com