
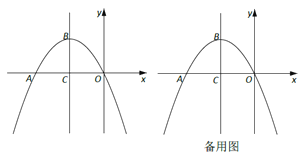
【题目】如图,在平面直角坐标系xOy中,抛物线![]() 与x轴负半轴交于点A,顶点为B,且对称轴与x轴交于点C。
与x轴负半轴交于点A,顶点为B,且对称轴与x轴交于点C。
(1)求点B的坐标(用含m的代数式表示);
(2)D为BD中点,直线AD交y轴于E,若点E的坐标为(0,2),求抛物线的解析式;
(3)在(2)的条件下,点M在直线BO上,且使得△AMC的周长最小,P在抛物线上,Q在直线BC上,若以A、M、P、Q为顶点的四边形是平行四边形,求点P的坐标。
【答案】(1)(![]() ,-
,- ![]() );(2)
);(2)![]() ;(3)P1(1,
;(3)P1(1, ![]() )、P2(-7,
)、P2(-7, ![]() )、P3(-5,
)、P3(-5, ![]() ).
).
【解析】试题解析:(1)利用配方法或公式法都能求出点B的坐标.
(2)可过点D作DF⊥x轴于F,那么DF是△BOC的中位线,由此得出DF、OF、CF的长;再由△AFD∽△AOE得出的比例线段以及OE的长,即可求出m的值,由此确定函数的解析式.
(3)此题中,首先要确定点M的位置:已知“△AMC的周长最小”,那么可作点C关于直线BO的对称点C′,连接AC′与直线BO的交点即为符合条件的点M;
确定点M后,由于所求平行四边形的四顶点顺序并不确定,所以分:AM为边和AM为对角线两种情况讨论;在解答时,可根据平行四边形的对边平行且相等的特点,过P、Q作坐标轴的垂线,通过构建全等三角形来确定点P的坐标.
试题解析:(1)∵y=![]() x22x=
x22x=![]() (x2mx+
(x2mx+![]() m2)
m2) ![]()
![]() m2=
m2=![]() (x
(x![]() m)2
m)2![]() m,
m,
∴抛物线的顶点B的坐标为(![]() m,
m,![]() m).
m).
(2)令![]() x22x=0,解得x1=0,x2=m.
x22x=0,解得x1=0,x2=m.
∵抛物线y=![]() x22x与x轴负半轴交于点A,
x22x与x轴负半轴交于点A,
∴A(m,0),且m<0.
过点span>D作DF⊥x轴于F,如图;

由D为BO中点,DF∥BC,可得CF=FO=![]() CO.
CO.
∴DF=![]() BC.
BC.
由抛物线的对称性得AC=OC.
∴AF:AO=3:4.
∵DF∥EO,
∴△AFD∽△AOE.
∴![]() .
.
由E(0,2),B(![]() m,
m,![]() m),得OE=2,DF=
m),得OE=2,DF=![]() m.
m.
∴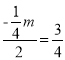 .
.
∴m=-6.
∴抛物线的解析式为y=![]() x22x.
x22x.
(3)依题意,得A(-6,0)、B(-3,3)、C(-3,0).可得直线OB的解析式为y=-x,直线BC为x=-3.
作点C关于直线BO的对称点C′(0,3),连接AC′交BO于M,则M即为所求.
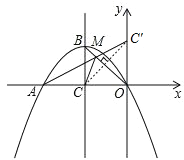
由A(-6,0),C′(0,3),可得直线AC′的解析式为y=![]() x+3.
x+3.
由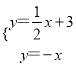
解得![]()
∴点M的坐标为(-2,2).
由点P在抛物线y=![]() x22x上,设P(t,
x22x上,设P(t,![]() t22t).
t22t).
(ⅰ)当AM为所求平行四边形的一边时.
①如图,过M作MG⊥x轴于G,过P1作P1H⊥BC于H,

则xG=xM=-2,xH=xB=-3.
∵四边形AMP1Q1为平行四边形,
∴AM=Pspan>1Q1,∠P1Q1H=∠AKC,
∵BK∥MG,
∴∠AMG=∠AKC,
∴∠P1Q1H=∠AMG,
∵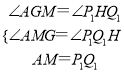 ,
,
∴△AMG≌△P1Q1H.
∴P1H=AG=4.
∴t-(-3)=4.
∴t=1.
∴P1(1,![]() ).
).
②如图,
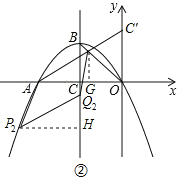
同①方法可得P2H=AG=4.
∴-3-t=4.
∴t=-7.
∴P2(7,![]() ).
).
(ⅱ)当AM为所求平行四边形的对角线时,如图;
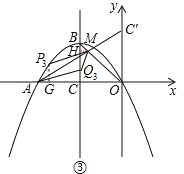
过M作MH⊥BC于H,过P3作P3G⊥x轴于G,则xH=xB=-3,xG=xP3=t.
由四边形AP3MQ3为平行四边形,可证△AP3G≌△MQ3H.
可得AG=MH=1.
∴t-(-6)=1.
∴t=-5.
∴P3(5, ![]() ).
).
综上,点P的坐标为P1(1, ![]() )、P2(7,
)、P2(7, ![]() )、P3(5,
)、P3(5, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】某商场对今年端午节这天销售A、B、C三种品牌粽子的情况进行了统计,绘制如图1和图2所示的统计图.根据图中信息解答下列问题:

(1)哪一种品牌粽子的销售量最大?
(2)补全图1中的条形统计图.
(3)写出A品牌粽子在图2中所对应的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大美山水“硒都恩施”是一张亮丽的名片,八方游客慕名而来,今年“五一”期间,恩施州共接待游客1450000人,将1450000用科学记数法表示为( )
A.0.145×106
B.14.5×105
C.1.45×105
D.1.45×106
查看答案和解析>>
科目:初中数学 来源: 题型:
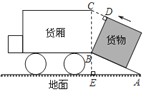
【题目】如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图。已知长方体货厢的高度BC为![]() 米,tanA=
米,tanA=![]() 。现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长。(结果保留根号)
。现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长。(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△DEF中,AB=AC,DE=DF,∠A=∠D。
(1)求证: ![]() ;
;
(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即![]() ,如T(60°)=1.
,如T(60°)=1.
①理解巩固:T(90°)= ,T(120°)= ,若α是等腰三角形的顶角,则T(α)的取值范围是 ;
②学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(精确到0.1)。
(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
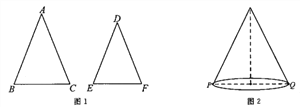
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长方形运动场被分隔成A,B,A,B,C共5个区,A区是边长为a m的正方形,C区是边长为c m的正方形.
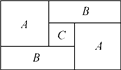
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40,c=10,求整个长方形运动场的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是10×8的网格,网格中每个小正方形的边长均为1,A、B两点在小正方形的顶点上,使以A、B、C为顶点的三角形分别满足以下要求: 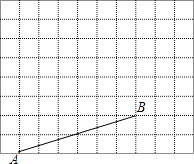
(1)请在图中取一点C(点C必须在小正方形的顶点上),使△ABC为钝角等腰三角形;
(2)通过计算,直接写出△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com