【题目】如图所示是10×8的网格，网格中每个小正方形的边长均为1，A、B两点在小正方形的顶点上，使以A、B、C为顶点的三角形分别满足以下要求：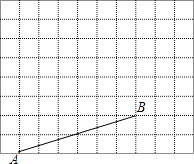 
（1）请在图中取一点C（点C必须在小正方形的顶点上），使△ABC为钝角等腰三角形；
（2）通过计算，直接写出△ABC的周长．
【答案】
（1）解：如图所示，△ABC为所求的三角形；
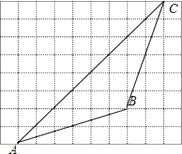
（2）解：由题意得：AB=BC= 
=2 
，
AC= 
=8 
，
则△ABC周长为4 +8
【解析】（1）如图所示，使AB=BC，连接AC，得到三角形ABC；（2）在网格中，利用勾股定理分别求出AB，BC以及AC的长，即可确定出三角形ABC周长．
【考点精析】根据题目的已知条件，利用等腰三角形的判定和勾股定理的概念的相关知识可以得到问题的答案，需要掌握如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
科目：初中数学 来源： 题型：
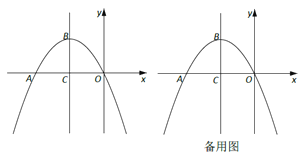
【题目】如图，在平面直角坐标系xOy中，抛物线
与x轴负半轴交于点A，顶点为B，且对称轴与x轴交于点C。
(1)求点B的坐标（用含m的代数式表示）；
(2)D为BD中点，直线AD交y轴于E，若点E的坐标为（0,2），求抛物线的解析式；
(3)在(2)的条件下，点M在直线BO上，且使得△AMC的周长最小，P在抛物线上，Q在直线BC上，若以A、M、P、Q为顶点的四边形是平行四边形，求点P的坐标。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，AB≠AD，对角线AC与BD相交于点O，OE⊥BD交AD于E，若△ABE的周长为12cm，则平行四边形ABCD的周长是（ ）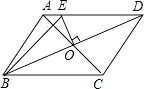 
A.40cm
B.24cm
C.48cm
D.无法确定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数： 
．
（1）设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？
（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？（成本＝进价×销售量）
查看答案和解析>>
科目：初中数学 来源： 题型：
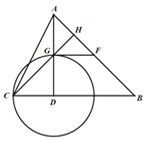
【题目】如图，在△ABC中，∠B=45°，AD⊥BC于点D，以D为圆心DC为半径作⊙D交AD于点G，过点G作⊙D的切线交AB于点F，且F恰好为AB中点.
（1）求tan∠ACD的值.
（2）连结CG并延长交AB于点H，若AH=2，求AC的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某物流公司承接A、B两种货物运输业务，已知5月份A货物运费单价为50元/吨，B货物运费单价为30元/吨，共收取运费9500元；6月份由于油价上涨，运费单价上涨为：A货物70元/吨，B货物40元/吨；该物流公司6月承接的A种货物和B种数量与5月份相同，6月份共收取运费13000元．
（1）该物流公司月运输两种货物各多少吨？
（2）该物流公司预计7月份运输这两种货物330吨，且A货物的数量不大于B货物的2倍，在运费单价与6月份相同的情况下，该物流公司7月份最多将收到多少运输费？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
