练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列计算正确的是（ ）
    A.a（a﹣1）=a2﹣a
    B.（a4）3=a7
    C.a4+a3=a7
    D.2a5÷a3=a2

    【答案】A
    【解析】解：A、原式=a2﹣a，符合题意； B、原式=a12 ， 不符合题意；
    C、原式不能合并，不符合题意；
    D、原式=2a2 ， 不符合题意，
    故选A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

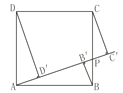
    【题目】如图，正方形ABCD的边长为1，点P为BC上任意一点（可与点B或C重合），分别过B、C、D作射线AP的垂线，垂足分别是B′、C′、D′，则BB′＋CC′＋DD′的最小值是（　　）

    A. 1 B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

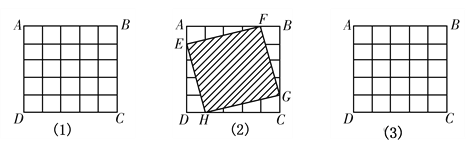
    【题目】如图(1)，在5×5正方形ABCD中，每个小正方形的边长都是1.

    (1)如图(2)，连结各条边上的四个点E，F，G，H可得到一个新的正方形，那么这个新正方形的边长是 ；

    (2)将新正方形做如下变换，点E向D点运动，同时点F以相同的速度向点A运动，其他两点也做相同变化；当E，F，G，H各点分别运动到AD，AB，BC，CD的什么位置时，所得的新正方形面积是13，在图(3)中画出新正方形，此时AE= ；

    (3)在图(1)中作出一条以A为端点的线段AP，使得线段AP=，且点P必须落在横纵线的交叉点上。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，∠A=30°，AB的垂直平分线分别交AB和AC于点D，E，AE=2，CE= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

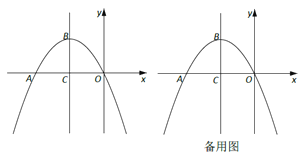
    【题目】如图，在平面直角坐标系xOy中，抛物线与x轴负半轴交于点A，顶点为B，且对称轴与x轴交于点C。

    　　(1)求点B的坐标（用含m的代数式表示）；

    　　(2)D为BD中点，直线AD交y轴于E，若点E的坐标为（0,2），求抛物线的解析式；

    　　(3)在(2)的条件下，点M在直线BO上，且使得△AMC的周长最小，P在抛物线上，Q在直线BC上，若以A、M、P、Q为顶点的四边形是平行四边形，求点P的坐标。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，E、F分别为边AB、CD的中点，BD是对角线，过A点作AG∥DB交CB的延长线于点G．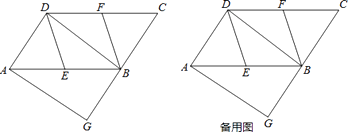

    （1）求证：DE∥BF；
    （2）若∠G=90°，求证：四边形DEBF是菱形；
    （3）请利用备用图分析，在（2）的条件下，若BE=4，∠DEB=120°，点M为BF的中点，当点P在BD边上运动时，求PF+PM的最小值，并求出此时线段BP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（﹣3，y1）、点B（﹣，y2）、点C（，y3）在该函数图象上，则y1＜y3＜y2；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x1和x2，且x1＜x2，则x1＜﹣1＜5＜x2．其中正确的结论有（　　）

    A. 2个 B. 3个 C. 4个 D. 5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，“中国海监50”正在南海海域A处巡逻，岛礁B上的中国海军发现点A在点B的正西方向上，岛礁C上的中国海军发现点A在点C的南偏东30°方向上，已知点C在点B的北偏西60°方向上，且B、C两地相距120海里．

    （1）求出此时点A到岛礁C的距离；

    （2）若“中海监50”从A处沿AC方向向岛礁C驶去，当到达点A′时，测得点B在A′的南偏东75°的方向上，求此时“中国海监50”的航行距离．（注：结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数： ．

    （1）设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？

    （2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？

    （3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？（成本＝进价×销售量）

    查看答案和解析>>

    同步练习册答案