Question

【题目】如图，在ABCD中，E、F分别为边AB、CD的中点，BD是对角线，过A点作AG∥DB交CB的延长线于点G．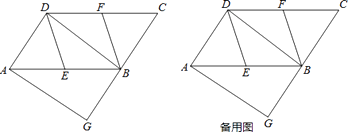

（1）求证：DE∥BF；
（2）若∠G=90°，求证：四边形DEBF是菱形；
（3）请利用备用图分析，在（2）的条件下，若BE=4，∠DEB=120°，点M为BF的中点，当点P在BD边上运动时，求PF+PM的最小值，并求出此时线段BP的长．

Answer 1

【答案】
（1）

证明：∵四边形ABCD是平行四边形，

∴AB=CD，AB∥CD，

∵E、F分别为边AB、CD的中点，

∴DF=BE，又AB∥CD，

∴四边形DEBF是平行四边形，

∴DE∥BF

（2）

证明：∵AG∥DB，AD∥CG，

∴四边形AGBD是平行四边形，

∵∠G=90°，

∴平行四边形AGBD是矩形，

∴∠ADB=90°，又E为边AB的中点，

∴ED=EB，又四边形DEBF是平行四边形，

∴四边形DEBF是菱形

（3）

解：连接EF，连接EM交BD于P，

∵四边形DEBF是菱形，

∴点E和点F关于BD轴对称，此时PF+PM的值最小，

∵四边形DEBF是菱形，∠DEB=120°，

∴∠EBF=60°，

∴△BEF是等边三角形，又BE=4，

∴EM=2 ，即PF+PM的最小值为2 ，

由题意得，点P为△EBF的重心，

∴BP= ．

【解析】（1）根据平行四边形的性质得到DF=BE，AB∥CD，根据平行四边形的判定定理证明四边形DEBF是平行四边形，根据平行四边形的性质证明结论；（2）根据矩形的判定定理得到四边形AGBD是矩形，根据直角三角形的性质得到ED=EB，证明结论；（3）连接EM交BD于P，根据轴对称的性质证明此时PF+PM的值最小，根据等边三角形的性质计算即可．
【考点精析】本题主要考查了平行四边形的性质和菱形的性质的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半才能正确解答此题．