
【题目】平行四边形ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,若CE=2,DF=1,∠EBF=60°,求平行四边形ABCD的面积. 
【答案】解:∵BE⊥CD,BF⊥AD, ∴∠BEC=∠BFD=90°,
∵∠EBF=60°,
∵∠D+∠BED+∠BFD+∠EBF=360°,
∴∠D=120°,
∵平行四边形ABCD,
∴DC∥AB,AD∥BC,∠A=∠C
∴∠A=∠C=180°﹣120°=60°,
∴∠ABF=∠EBC=30°,
∴AD=BC=2EC=4
在△BEC中由勾股定理得:BE=2 ![]() ,
,
在△ABF中AF=4﹣1=3,
∵∠ABF=30,
∴AB=6,
∴平行四边形ABCD的面积是ABBE=6×2 ![]() =12
=12 ![]() .
.
答:平行四边形ABCD的面积是12 ![]()
【解析】根据四边形的内角和等于360°,求出∠D=120°,根据平行四边形的性质得到∠A=∠C=60°,进一步求出∠ABF=∠EBC=30°,根据CE=2,DF=1,求出BC、AB的长,根据勾股定理求出BE的长,根据平行四边形的面积公式即可求出答案.
【考点精析】利用三角形的内角和外角和含30度角的直角三角形对题目进行判断即可得到答案,需要熟知三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.
(1)设AM交BC于点D,DE⊥AB于点E,DF⊥AC于点F,连接EF.有以下三种“判断”:
判断1:AD垂直平分EF.
判断2:EF垂直平分AD.
判断3:AD与EF互相垂直平分.
你同意哪个“判断”?简述理由;
(2)若射线AM上有一点N到△ABC的顶点B,C的距离相等,连接NB,NC.
①请指出△NBC的形状,并说明理由;
②当AB=11,AC=7时,求四边形ABNC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在5×5正方形ABCD中,每个小正方形的边长都是1.
(1)如图(2),连结各条边上的四个点E,F,G,H可得到一个新的正方形,那么这个新正方形的边长是 ;
(2)将新正方形做如下变换,点E向D点运动,同时点F以相同的速度向点A运动,其他两点也做相同变化;当E,F,G,H各点分别运动到AD,AB,BC,CD的什么位置时,所得的新正方形面积是13,在图(3)中画出新正方形,此时AE= ;
(3)在图(1)中作出一条以A为端点的线段AP,使得线段AP=![]() ,且点P必须落在横纵线的交叉点上。
,且点P必须落在横纵线的交叉点上。
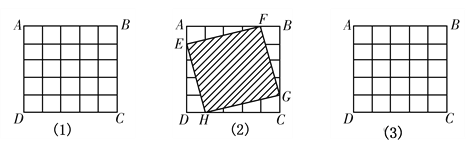
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.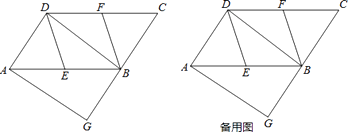
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形;
(3)请利用备用图分析,在(2)的条件下,若BE=4,∠DEB=120°,点M为BF的中点,当点P在BD边上运动时,求PF+PM的最小值,并求出此时线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有500名学生参加毕业会考,其数学成绩在90~100分之间的共有180人,则这个分数段的频率为( )
A. 0.06 B. 0.12 C. 0.18 D. 0.36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com